题目内容
若曲线y=x3+ax在原点处的切线方程是2x-y=0,则实数a= .
【答案】分析:根据切线是2x-y=0,得到切线的斜率k=2,然后利用导数得a的数值.
解答:解:函数的导数为f'(x)=2x2+a,
因为在原点处的切线方程是2x-y=0,所以切线的斜率k=2,
即f'(0)=2,即a=2.
故答案为:2.
点评:本题主要考查导数的几何意义,利用切线方程得到切线斜率是解决本题的关键.
解答:解:函数的导数为f'(x)=2x2+a,
因为在原点处的切线方程是2x-y=0,所以切线的斜率k=2,
即f'(0)=2,即a=2.
故答案为:2.
点评:本题主要考查导数的几何意义,利用切线方程得到切线斜率是解决本题的关键.

练习册系列答案
相关题目
 =________.
=________.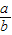 = .
= .