题目内容
已知双曲线的顶点与焦点分别是椭圆 的焦点与顶点,若双曲线的离心率为2,则椭圆离心率为
的焦点与顶点,若双曲线的离心率为2,则椭圆离心率为
- A.

- B.

- C.

- D.

B
分析:先根据双曲线的顶点与焦点分别是椭圆的焦点与顶点,确定双曲线的顶点与焦点,由双曲线的离心率求出椭圆的离心率.
解答:由题意可设双曲线的方程为:
∵椭圆 的焦点(±c,0),顶点(±a,0),c2=a2-b2
的焦点(±c,0),顶点(±a,0),c2=a2-b2
由题意可得,双曲线的顶点为(±c,0),焦点为(±a,0)
∴m=c,n2+m2=a2
∵双曲线的离心率e=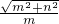 =2
=2
∴n=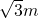
∴b=n=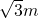 ,c=m,a=2m
,c=m,a=2m
椭圆的离心率e=
故选B
点评:本题以椭圆方程为载体,考查双曲线的几何性质,考查椭圆的离心率,正确运用几何量的关系是关键.
分析:先根据双曲线的顶点与焦点分别是椭圆的焦点与顶点,确定双曲线的顶点与焦点,由双曲线的离心率求出椭圆的离心率.
解答:由题意可设双曲线的方程为:

∵椭圆
 的焦点(±c,0),顶点(±a,0),c2=a2-b2
的焦点(±c,0),顶点(±a,0),c2=a2-b2由题意可得,双曲线的顶点为(±c,0),焦点为(±a,0)
∴m=c,n2+m2=a2
∵双曲线的离心率e=
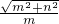 =2
=2∴n=
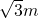
∴b=n=
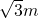 ,c=m,a=2m
,c=m,a=2m椭圆的离心率e=

故选B
点评:本题以椭圆方程为载体,考查双曲线的几何性质,考查椭圆的离心率,正确运用几何量的关系是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的方程为
的方程为  ,双曲线
,双曲线 的左、右焦
的左、右焦 与双曲线C2恒有两个不同的交点A和B,求
与双曲线C2恒有两个不同的交点A和B,求 的范围。
的范围。