题目内容

若f（x）=ax+b一个零点2，则g（x）=bx2-ax的零点是（　　）
A．0或2B．0或
1
2
C．0或-
1
2
D．2或1
∵函数f（x）=ax+b（a≠0）有一个零点是2，
∴2a+b=0．
故g（x）=bx2-ax=bx2+
1
2
bx=bx（x+
1
2
），
令bx（x+
1
2
）=0，可得x=0，或 x=-
1
2
．
故g（x）=bx2-ax的零点是0和-
1
2
，
故选C．
练习册系列答案
相关题目
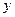某单位建造一间地面面积为12m2的背面靠墙的矩形小房，由于地理位置的限制，房子侧面的长度x不得超过a米，房屋正面的造价为400元/m2,房屋侧面的造价为150元/m2，屋顶和地面的造价费用合计为5800元，如果墙高为3m，且不计房屋背面的费用．
（1）把房屋总造价表示成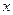的函数，并写出该函数的定义域.
（2）当侧面的长度为多少时，总造价最底？最低总造价是多少？
已知二次函数y=g（x）的导函数的图象与直线y=2x平行，且y=g（x）在x=-1处取得极小值m-1（m≠0）．设f(x)=
g(x)
x
．
（1）若曲线y=f（x）上的点P到点Q（0，2）的距离的最小值为
2
，求m的值；
（2）k（k∈R）如何取值时，函数y=f（x）-kx存在零点，并求出零点．
方程x5-x-1=0的一个零点存在的区间可能是______．（端点值为整数）
函数f（x）=lnx+x-2的零点个数是（　　）
A．0B．1C．2D．3
关于x的方程|x2-2x|+m+1=0有两个不相等的实数根，则m的取值范围是 ______．
已知函数f(x)=
x+
1
2
，x∈[0，
1
2
)
3x2，x∈[
1
2
，1]
，若存在x1＜x2，使得f（x1）=f（x2），则x1•f（x2）的取值范围为（　　）
A．[
3
4
，1)		B．[
1
8
，
3
6
)		C．[
3
16
，
1
2
)		D．[
3
8
，3)
已知
2
＜a＜2，则函数f（x）=
a2-x2
+|x|-2的零点个数为（　　）
A．1B．2C．3D．4
函数f（x）=3x+x在下列哪个区间内有零点（　　）
A．[-2，-1]B．[-1，0]C．[0，1]D．[1，2]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网