题目内容
设曲线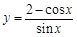 在点
在点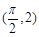 处的切线与直线
处的切线与直线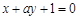 垂直,则
垂直,则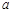 等于
等于
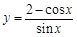 在点
在点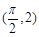 处的切线与直线
处的切线与直线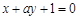 垂直,则
垂直,则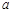 等于
等于| A.2 | B.-2 | C.1 | D.-1 |
C
分析:求出曲线解析式的导函数,把x等于 代入导函数即可求出切线的斜率,再表示出已知直线的斜率,根据两直线垂直时斜率的乘积为-1,列出关于a的方程,求出方程的解即可得到a的值.
代入导函数即可求出切线的斜率,再表示出已知直线的斜率,根据两直线垂直时斜率的乘积为-1,列出关于a的方程,求出方程的解即可得到a的值.
解答:解:y’= ,所以切线斜率k=f′(
,所以切线斜率k=f′( )=1,所以x+ay+1=0的斜率为-1,
)=1,所以x+ay+1=0的斜率为-1,
即- =-1,解得a=1.
=-1,解得a=1.
故选C
 代入导函数即可求出切线的斜率,再表示出已知直线的斜率,根据两直线垂直时斜率的乘积为-1,列出关于a的方程,求出方程的解即可得到a的值.
代入导函数即可求出切线的斜率,再表示出已知直线的斜率,根据两直线垂直时斜率的乘积为-1,列出关于a的方程,求出方程的解即可得到a的值.解答:解:y’=
 ,所以切线斜率k=f′(
,所以切线斜率k=f′( )=1,所以x+ay+1=0的斜率为-1,
)=1,所以x+ay+1=0的斜率为-1,即-
 =-1,解得a=1.
=-1,解得a=1.故选C

练习册系列答案
相关题目
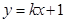 与曲线
与曲线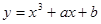 切于点(1, 3),则b的值为()
切于点(1, 3),则b的值为()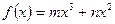 (
(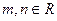 )在
)在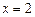 时有极值,其图象在点
时有极值,其图象在点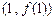 处的切线与直线
处的切线与直线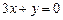 平行。
平行。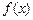 的单调区间。
的单调区间。
 ( )
( )


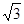
 在点
在点 处的切线方程为
处的切线方程为




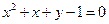 ,则下列
,则下列 各点中在曲线C上的点是( )
各点中在曲线C上的点是( ) 是曲线C:
是曲线C: 上的一点,过点
上的一点,过点 平行于直线
平行于直线 ,则切线
,则切线


 或
或 ,若
,若 ,则
,则 ( )
( )


