题目内容
已知二次函数 的导函数的图像与直线
的导函数的图像与直线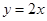 平行,且
平行,且 在
在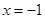 处取得极小值
处取得极小值 .设
.设 .
.
(1)若曲线 上的点
上的点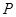 到点
到点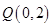 的距离的最小值为
的距离的最小值为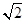 ,求
,求 的值;
的值;
(2)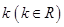 如何取值时,函数
如何取值时,函数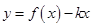 存在零点,并求出零点.
存在零点,并求出零点.
【答案】
(1)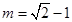 或
或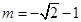 ;(2)详见解析.
;(2)详见解析.
【解析】
试题分析:(1)先设点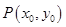 的坐标,利用两点间的距离公式将
的坐标,利用两点间的距离公式将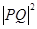 表示为
表示为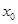 为自变量的函数,利用基本不等式求出相应的最小值,然后列方程求出
为自变量的函数,利用基本不等式求出相应的最小值,然后列方程求出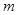 的值;(2)令
的值;(2)令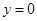 ,将函数
,将函数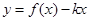 的零点转化为求方程
的零点转化为求方程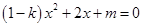 的根,对首项系数
的根,对首项系数 的符号进行分类讨论,以及在首项系数不为零时对
的符号进行分类讨论,以及在首项系数不为零时对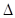 的符号进行分类讨论,从而确定函数在定义域上是否存在零点,并且在零点存在的前提下利用求根公式求出相应的零点值.
的符号进行分类讨论,从而确定函数在定义域上是否存在零点,并且在零点存在的前提下利用求根公式求出相应的零点值.
试题解析:(1)依题可设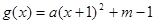 (
( ),则
),则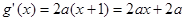 ;
;
又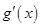 的图像与直线
的图像与直线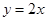 平行
平行 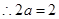
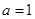
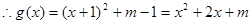 ,
,
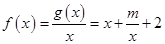 ,
,
设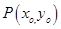 ,则
,则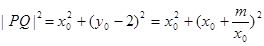
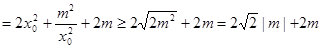
当且仅当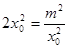 时,
时, 取得最小值,即
取得最小值,即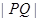 取得最小值
取得最小值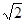
当 时,
时, 解得
解得
当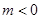 时,
时,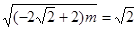 解得
解得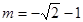
(2)由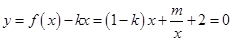 (
( ),得
),得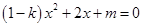

当 时,方程
时,方程 有一解
有一解 ,函数
,函数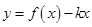 有一零点
有一零点 ;
;
当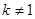 时,方程
时,方程 有二解
有二解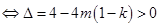 ,
,
若 ,
,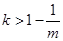 ,
,
函数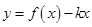 有两个零点
有两个零点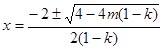 ,即
,即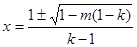 ;
;
若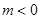 ,
,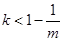 ,
,
函数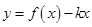 有两个零点
有两个零点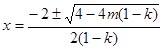 ,即
,即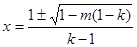 ;
;
当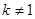 时,方程
时,方程 有一解
有一解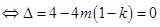 ,
, 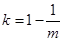 ,
,
函数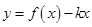 有一零点
有一零点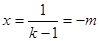
综上,当 时, 函数
时, 函数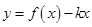 有一零点
有一零点 ;
;
当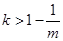 (
( ),或
),或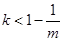 (
(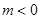 )时,
)时,
函数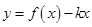 有两个零点
有两个零点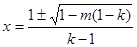 ;
;
当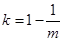 时,函数
时,函数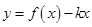 有一零点
有一零点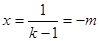 .
.
考点:1.两点间的距离公式;2.基本不等式;3.分类讨论;4.一元二次方程的求解

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
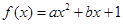 的导函数为
的导函数为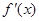 ,
, ,f(x)与x轴恰有一个交点,则
,f(x)与x轴恰有一个交点,则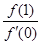 的最小值为 ( )
的最小值为 ( ) 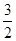 C.3 D.
C.3 D.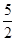
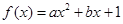 的导函数为
的导函数为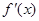 ,
,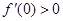 ,f(x)与x轴恰有一个交点,则
,f(x)与x轴恰有一个交点,则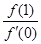 的最小值为( )
的最小值为( )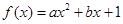 的导函数为
的导函数为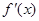 ,
,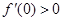 ,f(x)与x轴恰有一个交点,则
,f(x)与x轴恰有一个交点,则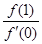 的最小值为 ( )
的最小值为 ( )