题目内容
(本题满分14分)
已知椭圆![]() 、抛物线
、抛物线![]() 的焦点均在
的焦点均在![]() 轴上,
轴上,![]() 的中心和
的中心和![]() 的顶点均为原点
的顶点均为原点![]() ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:
|
| 1 |
| 2 |
|
|
|
| 0 |
|
|
(Ⅰ)求![]() 的标准方程;
的标准方程;
(Ⅱ)过点曲线的![]() 的焦点
的焦点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于M、N两点,与
交于M、N两点,与![]() 轴交于E点,
轴交于E点,
若![]() 为定值。
为定值。
(本题满分14分)
解:(Ⅰ)设抛物线![]() ,则有
,则有![]() ,据此验证
,据此验证![]() 个点知(1,
个点知(1,![]() )、(2,
)、(2,![]() 4)在抛物线上,易求
4)在抛物线上,易求![]() ………………2分
………………2分
设![]() :
:![]() ,把点(
,把点(![]()
![]() ,0)(
,0)(![]() ,
,![]() )代入得:
)代入得:
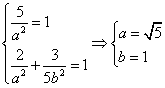
![]() 方程为
方程为![]() ………………………………………………………5分
………………………………………………………5分
(Ⅱ)证明:设![]() 点的坐标分别为
点的坐标分别为![]() ,
,
又易知![]() 点的坐标为
点的坐标为![]() .且点
.且点![]() 在椭圆
在椭圆![]() 内, 故过点
内, 故过点![]() 的直线l必与椭圆相交.
的直线l必与椭圆相交.
∵![]() , ∴
, ∴![]() .
.
∴ ![]() ,
,![]() . ………………………………………………8分
. ………………………………………………8分
将M点坐标代入到椭圆方程中得:![]() ,
,
去分母整理,得![]() . ………………………………………10分
. ………………………………………10分
同理,由![]() 可得:
可得:![]() . ………………………12分
. ………………………12分
∴ ![]() ,
,![]() 是方程
是方程![]() 的两个根, ∴
的两个根, ∴ ![]() .………14分
.………14分

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 B=[0,3],求实数m的值
B=[0,3],求实数m的值 CRB,求实数m的取值范围
CRB,求实数m的取值范围 是⊙
是⊙ :
: 上的任意一点,过
上的任意一点,过 垂直
垂直 轴于
轴于 ,动点
,动点 满足
满足 。
。 ,在动点
,在动点 、
、 ,使
,使 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。 .
. 的定义域;
的定义域; 是否有根?如果有根
是否有根?如果有根 ,请求出一个长度为
,请求出一个长度为 的区间
的区间 ,使
,使
 ).
).