题目内容
某村计划建造一个室内面积为800m2的矩形蔬菜温室。在温室内，沿左、右两侧与后侧内墙各保留1宽的通道，沿前侧内墙保留3m宽的空地。当矩形温室的长、宽各为多少时，蔬菜的种植面积最大？最大种植面积是多少？
解：设矩形温室的左侧边长为a m，后侧边长为b m，则 ab=800，
蔬菜的种植面积S=（a-4）（b-2）=ab-4b-2a+8=808-2（a+2b）
因为a+2b≥2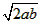
，
所以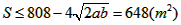
，
当且仅当a=2b，即a=40（m），b=20（m），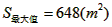
答：当矩形温室的左侧边长为40m，后侧边长为20m时，蔬菜的种植面积最大，最大种植面积为648m2。
蔬菜的种植面积S=（a-4）（b-2）=ab-4b-2a+8=808-2（a+2b）
因为a+2b≥2
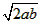， 所以
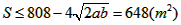，当且仅当a=2b，即a=40（m），b=20（m），
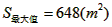
答：当矩形温室的左侧边长为40m，后侧边长为20m时，蔬菜的种植面积最大，最大种植面积为648m2。
练习册系列答案
优学名师名题系列答案
相关题目
某村计划建造一个室内面积为800m2的矩形蔬菜温室．在温室内，沿左、右两侧与后侧内墙各保留1m宽的通道，沿前侧内墙保留3m宽的空地．当矩形温室的边长各为多少时？蔬菜的种植面积最大？最大种植面积是多少？
在新农村建设过程中，某村计划建造一个室内矩形（ABCD）蔬菜温室．在温室内，沿左、右两侧与后侧内墙各保留1m宽的通道，沿前侧内墙保留3m宽的空地，内部（EFGH）种植蔬菜（示意图）．
某村计划建造一个室内面积为800m2的矩形蔬菜温室．在温室内，种植蔬菜时需要沿左、右两侧与前侧内墙各保留1m宽的空地作为通道，后侧内墙不留空地（如图所示），问当温室的长是多少米时，能使蔬菜的种植面积最大？
某村计划建造一个室内面积为800m2的矩形蔬菜温室（如图）．在温室内，沿左、右两侧与后侧内墙各保留1m宽的通道，沿前侧内墙保留3m宽的空地．设矩形温室的左侧边长为am，后侧边长为bm，蔬菜的种植面积为Sm2．
某村计划建造一个室内面积为800m2的矩形蔬菜温室．在温室内，沿左、右两侧与后侧内墙各保留1m宽的通道，沿前侧内墙保留3m宽的空地，设矩形温室的一边长为xm，蔬菜的种植面积为Sm2（如图所示）．