题目内容
已知A1,A2为双曲线C: 的左右两个顶点,一条动弦垂直于x轴,且与双曲线交于P,Q(P点位于x轴的上方),直线A1P与直线A2Q相交于点M,
的左右两个顶点,一条动弦垂直于x轴,且与双曲线交于P,Q(P点位于x轴的上方),直线A1P与直线A2Q相交于点M,
(1)求出动点M(2)的轨迹方程
(2)设点N(﹣2,0),过点N的直线交于M点的轨迹上半部分A,B两点,且满足 ,其中
,其中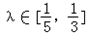 ,求出直线AB斜率的取值范围.
,求出直线AB斜率的取值范围.
 的左右两个顶点,一条动弦垂直于x轴,且与双曲线交于P,Q(P点位于x轴的上方),直线A1P与直线A2Q相交于点M,
的左右两个顶点,一条动弦垂直于x轴,且与双曲线交于P,Q(P点位于x轴的上方),直线A1P与直线A2Q相交于点M,(1)求出动点M(2)的轨迹方程
(2)设点N(﹣2,0),过点N的直线交于M点的轨迹上半部分A,B两点,且满足
 ,其中
,其中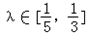 ,求出直线AB斜率的取值范围.
,求出直线AB斜率的取值范围.解:(1)设P(x0,y0),Q(x0,﹣y0),
直线A1P的方程为: ,(1)
,(1)
直线A2Q的方程为: ,(2)
,(2)
将(1)×(2)得到: ,又因为
,又因为 .
.
所以得到M的轨迹方程为: ,(y≠0)
,(y≠0)
(2) ,∴A,B,N三点共线,而点N的坐标为(﹣2,0).
,∴A,B,N三点共线,而点N的坐标为(﹣2,0).
设直线AB的方程为y=k(x+2),其中k为直线AB的斜率,依条件知k≠0.
由 消去x得
消去x得 ,
,
即
根据条件可知 解得
解得
设A(x1,y1),B(x2,y2),
则根据韦达定理,得
又由 得(x1+2,y1)=λ(x2+2,y2)
得(x1+2,y1)=λ(x2+2,y2)
 从而
从而
消去y2得
令
则
由于
所以φ(λ)是区间 上的减函数,
上的减函数,
从而 ,
,
即 ,
, ,
,
∴
解得
而 ,
,
∴
因此直线AB的斜率的取值范围是 。
。

直线A1P的方程为:
 ,(1)
,(1)直线A2Q的方程为:
 ,(2)
,(2)将(1)×(2)得到:
 ,又因为
,又因为 .
.所以得到M的轨迹方程为:
 ,(y≠0)
,(y≠0)(2)
 ,∴A,B,N三点共线,而点N的坐标为(﹣2,0).
,∴A,B,N三点共线,而点N的坐标为(﹣2,0).设直线AB的方程为y=k(x+2),其中k为直线AB的斜率,依条件知k≠0.
由
 消去x得
消去x得 ,
,即

根据条件可知
 解得
解得
设A(x1,y1),B(x2,y2),
则根据韦达定理,得

又由
 得(x1+2,y1)=λ(x2+2,y2)
得(x1+2,y1)=λ(x2+2,y2) 从而
从而
消去y2得

令

则

由于

所以φ(λ)是区间
 上的减函数,
上的减函数,从而
 ,
,即
 ,
, ,
,∴

解得

而
 ,
,∴

因此直线AB的斜率的取值范围是
 。
。
练习册系列答案
 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 的左右两个顶点,一条动弦垂直于x轴,且与双曲线交于P,Q(P点位于x轴的上方),直线A1P与直线A2Q相交于点M,
的左右两个顶点,一条动弦垂直于x轴,且与双曲线交于P,Q(P点位于x轴的上方),直线A1P与直线A2Q相交于点M,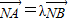 ,其中
,其中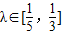 ,求出直线AB斜率的取值范围.
,求出直线AB斜率的取值范围.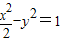 的左右两个顶点,一条动弦垂直于x轴,且与双曲线交于P,Q(P点位于x轴的上方),直线A1P与直线A2Q相交于点M,
的左右两个顶点,一条动弦垂直于x轴,且与双曲线交于P,Q(P点位于x轴的上方),直线A1P与直线A2Q相交于点M,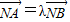 ,其中
,其中 ,求出直线AB斜率的取值范围.
,求出直线AB斜率的取值范围.