题目内容
已知A1,A2为双曲线C:
-y2=1的左右两个顶点,一条动弦垂直于x轴,且与双曲线交于P,Q(P点位于x轴的上方),直线A1P与直线A2Q相交于点M,
(1)求出动点M(2)的轨迹方程
(2)设点N(-2,0),过点N的直线交于M点的轨迹上半部分A,B两点,且满足
=λ
,其中λ∈[
,
],求出直线AB斜率的取值范围.
| x2 |
| 2 |
(1)求出动点M(2)的轨迹方程
(2)设点N(-2,0),过点N的直线交于M点的轨迹上半部分A,B两点,且满足
| NA |
| NB |
| 1 |
| 5 |
| 1 |
| 3 |
(1)设P(x0,y0),Q(x0,-y0),A1(-
,0),A2(
,0)
直线A1P的方程为:
=
,(1)
直线A2Q的方程为:
=
,(2)
将(1)×(2)得到:
=
,又因为
-y02=1.
所以得到M的轨迹方程为:
+y2=1,(y≠0)
(2)
=λ
,∴A,B,N三点共线,而点N的坐标为(-2,0).
设直线AB的方程为y=k(x+2),其中k为直线AB的斜率,依条件知k≠0.
由
消去x得(
y-2)2+2 y2=2,即
y2-
y+2=0
根据条件可知
解得0<|k|<
(5分)
设A(x1,y1),B(x2,y2),则根据韦达定理,得
又由
=λ
得(x1+2,y1)=λ(x2+2,y2)
从而
消去y2得
=
消去
令∅(λ)=
,λ∈[
,
]则∅′(λ)=1-
=
由于
≤λ≤
所以∅(λ)是区间[
,
]上的减函数,
从而∅(
)≤∅(λ)≤∅(
),即
≤∅(λ)≤
,
≤
≤
,∴
≤
≤
解得
≤|k|≤
而0<k<
,∴
≤k≤
因此直线AB的斜率的取值范围是[
,
]
| 2 |
| 2 |
直线A1P的方程为:
| y |
| y0 |
x+
| ||
x0+
|
直线A2Q的方程为:
| y |
| -y0 |
x-
| ||
x0-
|
将(1)×(2)得到:
| y2 |
| -y02 |
| x2-2 |
| x02-2 |
| x02 |
| 2 |
所以得到M的轨迹方程为:
| x2 |
| 2 |
(2)
| NA |
| NB |
设直线AB的方程为y=k(x+2),其中k为直线AB的斜率,依条件知k≠0.
由
|
| 1 |
| k |
| 2k2+1 |
| k2 |
| 4 |
| k |
根据条件可知
|
| ||
| 2 |
设A(x1,y1),B(x2,y2),则根据韦达定理,得
|
又由
| NA |
| NB |
|
|
| (1+λ)2 |
| λ |
| 8 |
| 2k2+1 |
令∅(λ)=
| (1+λ)2 |
| λ |
| 1 |
| 5 |
| 1 |
| 3 |
| 1 |
| λ2 |
| λ2-1 |
| λ2 |
由于
| 1 |
| 5 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 3 |
从而∅(
| 1 |
| 3 |
| 1 |
| 5 |
| 16 |
| 3 |
| 36 |
| 5 |
| 16 |
| 3 |
| 8 |
| 2k2+1 |
| 36 |
| 5 |
| 16 |
| 3 |
| 8 |
| 2k2+1 |
| 36 |
| 5 |
| ||
| 6 |
| 1 |
| 2 |
而0<k<
| ||
| 2 |
| ||
| 6 |
| 1 |
| 2 |
因此直线AB的斜率的取值范围是[
| ||
| 6 |
| 1 |
| 2 |

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 的左右两个顶点,一条动弦垂直于x轴,且与双曲线交于P,Q(P点位于x轴的上方),直线A1P与直线A2Q相交于点M,
的左右两个顶点,一条动弦垂直于x轴,且与双曲线交于P,Q(P点位于x轴的上方),直线A1P与直线A2Q相交于点M, ,其中
,其中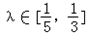 ,求出直线AB斜率的取值范围.
,求出直线AB斜率的取值范围. 的左右两个顶点,一条动弦垂直于x轴,且与双曲线交于P,Q(P点位于x轴的上方),直线A1P与直线A2Q相交于点M,
的左右两个顶点,一条动弦垂直于x轴,且与双曲线交于P,Q(P点位于x轴的上方),直线A1P与直线A2Q相交于点M,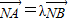 ,其中
,其中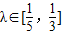 ,求出直线AB斜率的取值范围.
,求出直线AB斜率的取值范围.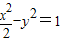 的左右两个顶点,一条动弦垂直于x轴,且与双曲线交于P,Q(P点位于x轴的上方),直线A1P与直线A2Q相交于点M,
的左右两个顶点,一条动弦垂直于x轴,且与双曲线交于P,Q(P点位于x轴的上方),直线A1P与直线A2Q相交于点M,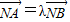 ,其中
,其中 ,求出直线AB斜率的取值范围.
,求出直线AB斜率的取值范围.