题目内容
函数y=f(x)在定义域R内可导,若f(x)=f(2-x),且当x∈(-∞,1)时,(x-1)f′(x)＜0,设a=f(0),b=f(
),c=f(3),则A.a＜b＜c B.c＜a＜b C.c＜b＜a D.b＜c＜a
B ∵f(x)=f(2-x),∴f(x)的对称轴为x=
=1.
又∵当x∈(-∞,1)时,(x-1)·f′(x)＜0,∴当x∈(-∞,1)时,f′(x)＞0.
∴当x∈(1,+∞)时,f′(x)＜0.
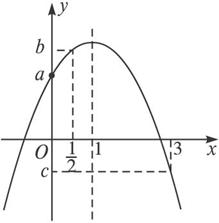
∴f(x)的图象及a、b、c的关系大致如上图所示.可知c＜a＜b.
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
(a,b∈Z)，曲线y=f(x)在点（2，f(2)）处的切线方程为y=3。
（a,b∈Z），曲线y=f(x)在点（2，f（2））处的切线方程为y=3.
(a,b∈Z)，曲线y=f(x)在点（2，f(2)）处的切线方程为y=3。
（2）根据k的取值范围，确定y=f(x)的定义域.