Question

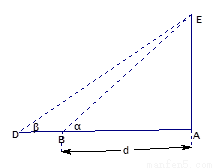
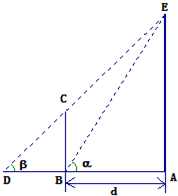某兴趣小组测量电视塔AE的高度H（单位：m），如示意图，垂直放置的标杆BC的高度h=4m，仰角∠ABE=α，∠ADE=β．
（1）该小组已经测得一组α、β的值，tanα=1.24，tanβ=1.20，请据此算出H的值；
（2）该小组分析若干测得的数据后，认为适当调整标杆到电视塔的距离d（单位：m），使α与β之差较大，可以提高测量精确度．若电视塔的实际高度为125m，试问d为多少时，α-β最大？

Answer 1

分析：（1）在Rt△ABE中可得AD=

H

tanβ

，在Rt△ADE中可得AB=

H

tanα

，BD=

h

tanβ

，再根据AD-AB=DB即可得到H．
（2）先用d分别表示出tanα和tanβ，再根据两角和公式，求得tan（α-β）=

h

d+ H(H-h) d

，再根据均值不等式可知当d=

H(H-h)

=

125×121

=55

5

时，tan（α-β）有最大值即α-β有最大值，得到答案．

解答：解：（1）

H

AD

=tanβ?AD=

H

tanβ

，同理：AB=

H

tanα

，BD=

h

tanβ

．
AD-AB=DB，故得

H

tanβ

-

H

tanα

=

h

tanβ

，
得：H=

htanα

tanα-tanβ

=

4×1.24

1.24-1.20

=124．
因此，算出的电视塔的高度H是124m．
（2）由题设知d=AB，得tanα=

H

d

，tanβ=

H

AD

=

h

DB

=

H-h

d

，
tan（α-β）=

tanα-tanβ

1+tanα•tanβ

=

H d - H-h d

1+ H d • H-h d

=

hd

d2+H(H-h)

=

h

d+ H(H-h) d

d+

H(H-h)

d

≥2

H(H-h)

，（当且仅当d=

H(H-h)

=

125×121

=55

5

时，取等号）
故当d=55

5

时，tan（α-β）最大．
因为0＜β＜α＜

π

2

，则0＜α-β＜

π

2

，所以当d=55

5

时，α-β最大．
故所求的d是55

5

m．

点评：本题主要考查解三角形的知识、两角差的正切及不等式的应用．当涉及最值问题时，可考虑用不等式的性质来解决．