Question

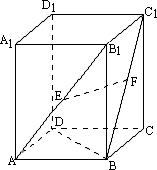
如下图，在正四棱柱ABCD-A₁B₁C₁D₁中，AB=1，BB₁=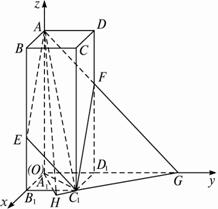+1，E为BB₁上使B₁E=1的点.平面AEC₁交DD₁于F，交A₁D₁的延长线于G，求：

（1）异面直线AD与C₁G所成的角的大小；

（2）二面角A—C₁G—A₁的正切值.

Answer 1

解：(1)以A₁为原点，A₁B₁，A₁D₁，A₁A所在直线分别为x轴，y轴和z轴建立如图所示的空间直角坐标系.于是，A（0，0，+1），C₁（1，1，0），D（0，1，+1），E（1，0，1），=（0，1，0），=（0，1，-1）.因为EC₁和AF分别是平行平面BB₁C₁C和AA₁D₁D与平面AEC₁G的交线，所以EC₁∥AF.??

设G（0，y,0）,则=（0，y，-（+1））.?

由∥得=,于是y=+1.?

故G（0，+1，0），=（-1，，0）.?

设异面直线AD与C₁G所成的角的大小为θ,则?

cosθ==.从而θ=.?

(2)作A₁H⊥C₁G交GC₁的延长线于H，由三垂线定理知AH⊥GH，故∠AHA₁为二面角A—C₁G—A₁的平面角.?

设H（a,b,0）,则?

=(a,b,0),=(a-1,b-1,0).?

由A₁H⊥C₁G得·=0，?

由此得a-b=0.              ①?

又由H、C₁、G共线得∥?

从而=,?

于是a+b-(+1)=0.            ②?

联立①和②得：a=,b=.?

故H（，，0）.?

由||==，?

||=+1得?

tan∠AHA₁===2.