题目内容
已知 为虚数单位,
为虚数单位, 为实数,复数
为实数,复数 在复平面内对应的点为
在复平面内对应的点为 ,则“
,则“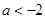 ”是“点
”是“点 在第四象限”的
在第四象限”的
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
A
解析试题分析:根据题意,由于复数 在复平面内对应的点为
在复平面内对应的点为 表示的点坐标为(2,-a),那么可知当a<-2时,则可知前者是后者的充分不必要条件,故选A
表示的点坐标为(2,-a),那么可知当a<-2时,则可知前者是后者的充分不必要条件,故选A
考点:复数的代数表示法及其几何意义
点评:本题考查复数的代数表示法及其几何意义,考查复数与复平面上的点的对应关系,考查不等式的解法,本题是一个基础题,注意要从两个方向验证条件是什么条件.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
设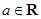 ,则“
,则“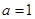 ”是“直线
”是“直线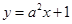 与直线
与直线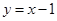 平行”的 ( )
平行”的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
在四边形 中,“
中,“ ,使得
,使得 ”是“四边形
”是“四边形 为平行四边形”的( )
为平行四边形”的( )
| A.充分而不必要条件 | B.必要而不充分条件 | C.充分必要条件 | D.既不充分也不必要条件 |
下列四个命题中,正确的是( )
A.已知 服从正态分布 服从正态分布 ,且 ,且 ,则 ,则 |
B.已知命题 ;命题 ;命题 .则命题“ .则命题“ ”是假命题 ”是假命题 |
C.设回归直线方程为 ,当变量 ,当变量 增加一个单位时, 增加一个单位时, 平均增加2个单位 平均增加2个单位 |
D.已知直线 , , ,则 ,则 的充要条件是 的充要条件是 =-3 =-3 |
下列命题中,为真命题的是( )
A. |
B. |
C. |
D. |
设 R,则“
R,则“ ”是“
”是“ ”( )
”( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
给出下面四个命题:
(1)如果直线 ,那么
,那么 可以确定一个平面;(2)如果直线
可以确定一个平面;(2)如果直线 和
和 都与直线
都与直线 相交,那么
相交,那么 可以确定一个平面;(3)如果
可以确定一个平面;(3)如果 那么
那么 可以确定一个平面;(4)直线
可以确定一个平面;(4)直线 过平面
过平面 内一点与平面外一点,直线
内一点与平面外一点,直线 在平面
在平面 内不经过该点,那么
内不经过该点,那么 和
和 是异面直线。上述命题中,真命题的个数是( )
是异面直线。上述命题中,真命题的个数是( )
| A.1个; | B.2个; | C.3个; | D.4个。 |
设 , 则 “
, 则 “ ”是“
”是“ ”的( )
”的( )
| A.充分而不必要条件 |
| B.必要而不充分条件 |
| C.充要条件 |
| D.既不充分也不必要条件 |
给定两个命题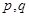 ,
,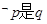 的必要而不充分条件,则
的必要而不充分条件,则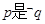 的( )
的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |