题目内容
设F1、F2为曲线C1:
+
=1的焦点,P是曲线C2:
-y2=1与C1的一个交点,则△PF1F2的面积为( )
| x2 |
| 6 |
| y2 |
| 2 |
| x2 |
| 3 |
分析:根据双曲线和椭圆的定义可得 PF1+PF2=2
,PF1-PF2=2
,△PF1F2中,由余弦定理可得cos∠F1PF2=
,故 sin∠F1PF2=
,
由△PF1F2的面积为
•PF1•PF2•sin∠F1PF2运算得到结果.
| 6 |
| 3 |
| 1 |
| 3 |
2
| ||
| 3 |
由△PF1F2的面积为
| 1 |
| 2 |
解答:解:由曲线C1:
+
=1的方程可得a=
,c=2,即F1 (-2,0)、F2(2,0),
再由椭圆的定义可得PF1+PF2=2
.
又因曲线C2:
-y2=1与C1的焦点相同,再由双曲线的定义可得
PF1-PF2=2
.
∴PF1=
+
,PF2=
-
.
△PF1F2中,由余弦定理可得 16=(
+
)2+(
-
)2-2(
+
)(
-
)cos∠F1PF2,
解得 cos∠F1PF2=
,
∴sin∠F1PF2=
,
△PF1F2的面积为
•PF1•PF2•sin∠F1PF2=
(
+
)(
-
)sin∠F1PF2=
,
故答案为:C.
| x2 |
| 6 |
| y2 |
| 2 |
| 6 |
再由椭圆的定义可得PF1+PF2=2
| 6 |
又因曲线C2:
| x2 |
| 3 |
PF1-PF2=2
| 3 |
∴PF1=
| 6 |
| 3 |
| 6 |
| 3 |
△PF1F2中,由余弦定理可得 16=(
| 6 |
| 3 |
| 6 |
| 3 |
| 6 |
| 3 |
| 6 |
| 3 |
解得 cos∠F1PF2=
| 1 |
| 3 |
∴sin∠F1PF2=
2
| ||
| 3 |
△PF1F2的面积为
| 1 |
| 2 |
| 1 |
| 2 |
| 6 |
| 3 |
| 6 |
| 3 |
| 2 |
故答案为:C.
点评:本题考查双曲线和椭圆的定义和标准方程,以及简单性质的应用,求出PF1=
+
,PF2=
-
,sin∠F1PF2 的值,是解题的关键.
| 6 |
| 3 |
| 6 |
| 3 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的值为
的值为 的焦点,P是曲线
的焦点,P是曲线 :
: 与C1的一个交点,
与C1的一个交点,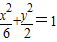 的焦点,P是曲线C2:
的焦点,P是曲线C2: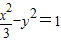 与C1的一个交点,则
与C1的一个交点,则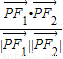 的值为( )
的值为( )



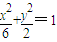 的焦点,P是曲线C2:
的焦点,P是曲线C2: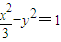 与C1的一个交点,则
与C1的一个交点,则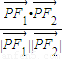 的值为( )
的值为( )



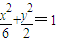 的焦点,P是曲线C2:
的焦点,P是曲线C2: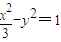 与C1的一个交点,则
与C1的一个交点,则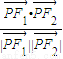 的值为( )
的值为( )


