题目内容
已知a＞0，函数
．设
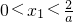，记曲线y=f（x）在点M（x1，f（x1））处的切线为l．
（Ⅰ）求l的方程；
（Ⅱ）设l与x轴交点为（x2，0）．证明：
①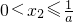
；
②若
，则
．
解：（I）求f（x）的导数：
，由此得切线l的方程：
．
（II）证：依题意，切线方程中令y=0，
．
①由
∴
．
②
．
分析：（I）欲求切线l的方程，则须求出它的斜率，根据切线斜率的几何意义便不难发现，问题归结为求曲线y=f（x）在点M（x1，f（x1））的一阶导数值．
（Ⅱ）①要求x2的变化范围，则须找到使x2产生变化的原因，显然，x2变化的根本原因可归结为x1的变化，因此，找到x2与x1的等量关系式，就成；②欲比较x2与x1的大小关系，判断它们的差的符号即可．
点评：本小题主要考查利用导数求曲线切线的方法，考查不等式的基本性质，以及分析和解决问题的能力．
，由此得切线l的方程：．（II）证：依题意，切线方程中令y=0，
．①由
∴
．②
．分析：（I）欲求切线l的方程，则须求出它的斜率，根据切线斜率的几何意义便不难发现，问题归结为求曲线y=f（x）在点M（x1，f（x1））的一阶导数值．
（Ⅱ）①要求x2的变化范围，则须找到使x2产生变化的原因，显然，x2变化的根本原因可归结为x1的变化，因此，找到x2与x1的等量关系式，就成；②欲比较x2与x1的大小关系，判断它们的差的符号即可．
点评：本小题主要考查利用导数求曲线切线的方法，考查不等式的基本性质，以及分析和解决问题的能力．
练习册系列答案
相关题目