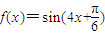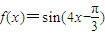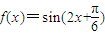题目内容
若将函数f（x）=x5表示为f（x）=a+a1（1+x）+a2（1+x）2+…+a5（1+x）5，其中a，a1，a2，…a5为实数，则a3= ．
【答案】分析：将x5转化[（x+1）-1]5，然后利用二项式定理进行展开，使之与f（x）=a+a1（1+x）+a2（1+x）2+…+a5（1+x）5进行比较，可得所求．
解答：解：f（x）=x5=[（x+1）-1]5=
（x+1）5+
（x+1）4（-1）+
（x+1）3（-1）2+
（x+1）2（-1）3+
（x+1）1（-1）4+
（-1）5
而f（x）=a+a1（1+x）+a2（1+x）2+…+a5（1+x）5，
∴a3=
（-1）2=10
故答案为：10
点评：本题主要考查了二项式定理的应用，解题的关键利用x5=[（x+1）-1]5展开，同时考查了计算能力，属于基础题．
解答：解：f（x）=x5=[（x+1）-1]5=
（x+1）5+（x+1）4（-1）+（x+1）3（-1）2+（x+1）2（-1）3+（x+1）1（-1）4+（-1）5而f（x）=a+a1（1+x）+a2（1+x）2+…+a5（1+x）5，
∴a3=
（-1）2=10故答案为：10
点评：本题主要考查了二项式定理的应用，解题的关键利用x5=[（x+1）-1]5展开，同时考查了计算能力，属于基础题．
练习册系列答案
相关题目
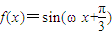（ω＞0）的图象的相邻两条对称轴间的距离是
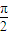．若将函数f（x）图象向右平移
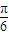个单位，得到函数g（x）的解析式为（ ）
