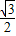Question

（文）椭圆的一个焦点与短轴的两端点构成一个正三角形，则该椭圆的离心率为（　　）

• A．

  3

  3

• B．

  1

  2

• C．

  3

  2

• D．不确定

Answer 1

分析：根据椭圆的短轴的两个端点与椭圆的一个焦点构成正三角形，得到a，b，c的关系，又根据椭圆的基本性质可知a²=b²+c²，把可用b表示出c，然后根据离心率e=

c

a

，分别把a与c的式子代入，约分后即可得到值．

解答：解：由题意，∵椭圆的短轴的两个端点与椭圆的一个焦点构成正三角形
∴

3

b=c，3b²=c²，
∵a²=b²+c²=

4

3

c2
∴e=

c

a

=

c2 a2

=

3 4

=

3

2

．
故选C．

点评：此题考查学生掌握椭圆的简单性质，考查了数形结合的数学思想，是一道综合题．