题目内容
已知向量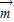 =
=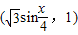 ,
,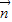 =
=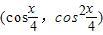 .
.(1)若
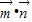 =1,求
=1,求 的值;
的值;(2)记函数f(x)=
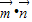 ,在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cosB=bcosC,求f(A)的取值范围.
,在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cosB=bcosC,求f(A)的取值范围.
【答案】分析:(1)由两向量的坐标及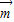 •
•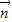 =1,利用平面向量的数量积运算法则列出关系式,利用二倍角的正弦、余弦函数公式化简,再利用两角和与差的正弦函数公式化为一个角的正弦函数,可得出sin(
=1,利用平面向量的数量积运算法则列出关系式,利用二倍角的正弦、余弦函数公式化简,再利用两角和与差的正弦函数公式化为一个角的正弦函数,可得出sin(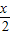 +
+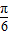 )的值,然后将所求式子利用二倍角的余弦函数公式化简后,将得出的sin(
)的值,然后将所求式子利用二倍角的余弦函数公式化简后,将得出的sin(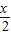 +
+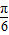 )的值代入即可求出值;
)的值代入即可求出值;
(2)利用正弦定理化简已知的等式,移项整理后再利用两角和与差的正弦函数公式及诱导公式变形后,根据sinA不为0,可得出cosB的值,由B为三角形的内角,利用特殊角的三角函数值求出B的度数,确定出A的范围,得出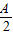 +
+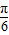 的范围,根据正弦函数的图象与性质得出sin(
的范围,根据正弦函数的图象与性质得出sin(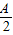 +
+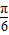 )的范围,即可得出f(A)的范围.
)的范围,即可得出f(A)的范围.
解答:解:(1)∵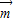 (
(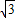 sin
sin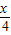 ,1),
,1),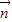 (cos
(cos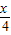 ,cos2
,cos2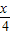 ),
),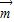 •
•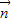 =1,
=1,
∴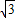 sin
sin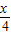 cos
cos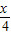 +cos2
+cos2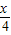 =1,…(2分)
=1,…(2分)
即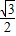 sin
sin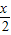 +
+ cos
cos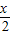 +
+ =1,
=1,
∴sin(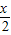 +
+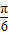 )=
)= ,…(4分)
,…(4分)
则cos(x+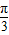 )=1-2sin2(
)=1-2sin2(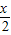 +
+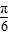 )=1-2•(
)=1-2•( )2=
)2= ;…(7分)
;…(7分)
(2)∵(2a-c)cosB=bcosC,
由正弦定理得(2sinA-sinC)cosB=sinBcocC,
∴2sinAcosB-sinCcosB=sinBcosC,
∴2sinAcosB=sin(B+C),…(9分)
∵A+B+C=π,
∴sin(B+C)=sinA,且sinA≠0,
∴cosB= ,即B=
,即B=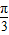 ,…(11分)
,…(11分)
∴0<A<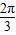 ,
,
∴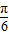 <
<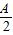 +
+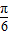 <
<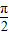 ,
,
∴ <sin(
<sin(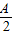 +
+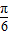 )<1,…(12分)
)<1,…(12分)
又∵f(x)=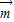 •
•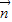 =sin(
=sin(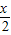 +
+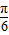 )+
)+ ,
,
∴f(A)=sin(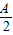 +
+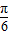 )+
)+ ,
,
∴1<f(A)< ,
,
则函数f(A)的取值范围是(1, ).…(14分)
).…(14分)
点评:此题考查了正弦定理,正弦函数的定义域与值域,平面向量的数量积运算法则,二倍角的正弦、余弦函数公式,两角和与差的正弦函数公式,诱导公式,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键.
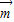 •
•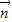 =1,利用平面向量的数量积运算法则列出关系式,利用二倍角的正弦、余弦函数公式化简,再利用两角和与差的正弦函数公式化为一个角的正弦函数,可得出sin(
=1,利用平面向量的数量积运算法则列出关系式,利用二倍角的正弦、余弦函数公式化简,再利用两角和与差的正弦函数公式化为一个角的正弦函数,可得出sin(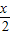 +
+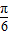 )的值,然后将所求式子利用二倍角的余弦函数公式化简后,将得出的sin(
)的值,然后将所求式子利用二倍角的余弦函数公式化简后,将得出的sin(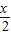 +
+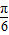 )的值代入即可求出值;
)的值代入即可求出值;(2)利用正弦定理化简已知的等式,移项整理后再利用两角和与差的正弦函数公式及诱导公式变形后,根据sinA不为0,可得出cosB的值,由B为三角形的内角,利用特殊角的三角函数值求出B的度数,确定出A的范围,得出
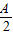 +
+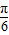 的范围,根据正弦函数的图象与性质得出sin(
的范围,根据正弦函数的图象与性质得出sin(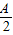 +
+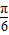 )的范围,即可得出f(A)的范围.
)的范围,即可得出f(A)的范围.解答:解:(1)∵
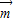 (
(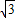 sin
sin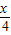 ,1),
,1),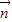 (cos
(cos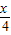 ,cos2
,cos2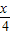 ),
),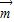 •
•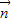 =1,
=1,∴
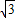 sin
sin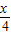 cos
cos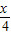 +cos2
+cos2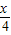 =1,…(2分)
=1,…(2分)即
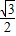 sin
sin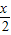 +
+ cos
cos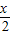 +
+ =1,
=1,∴sin(
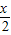 +
+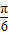 )=
)= ,…(4分)
,…(4分)则cos(x+
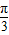 )=1-2sin2(
)=1-2sin2(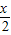 +
+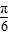 )=1-2•(
)=1-2•( )2=
)2= ;…(7分)
;…(7分)(2)∵(2a-c)cosB=bcosC,
由正弦定理得(2sinA-sinC)cosB=sinBcocC,
∴2sinAcosB-sinCcosB=sinBcosC,
∴2sinAcosB=sin(B+C),…(9分)
∵A+B+C=π,
∴sin(B+C)=sinA,且sinA≠0,
∴cosB=
 ,即B=
,即B=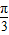 ,…(11分)
,…(11分)∴0<A<
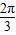 ,
,∴
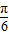 <
<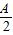 +
+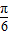 <
<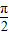 ,
,∴
 <sin(
<sin(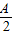 +
+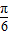 )<1,…(12分)
)<1,…(12分)又∵f(x)=
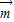 •
•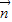 =sin(
=sin(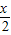 +
+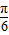 )+
)+ ,
,∴f(A)=sin(
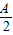 +
+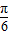 )+
)+ ,
,∴1<f(A)<
 ,
,则函数f(A)的取值范围是(1,
 ).…(14分)
).…(14分)点评:此题考查了正弦定理,正弦函数的定义域与值域,平面向量的数量积运算法则,二倍角的正弦、余弦函数公式,两角和与差的正弦函数公式,诱导公式,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
