Question

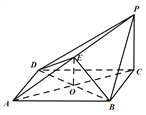
【题目】如图，在四棱锥中，底面为正方形，点是棱的中点，，平面平面．

（Ⅰ）求证：//平面；

（Ⅱ）求证：平面；

(Ⅲ) 设,试判断平面⊥平面能否成立；若成立，写出的一个值（只需写出结论）．

Answer 1

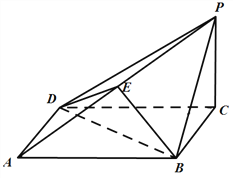
【答案】（Ⅰ）见解析; （Ⅱ）见解析(Ⅲ) 不能成立.

【解析】试题分析：

(1)由题意可得EO// PC，利用线面平行的判定定理可得PC//平面BDE；

(2) 利用题意证得PC⊥AC,PC⊥BD，结合线面垂直的判定定理即可证得结论；

(3)由空间关系可知面面垂直的关系不能成立.

试题解析：

证明：（Ⅰ）证明：设，连接，

因为底面为正方形，

所以是的中点，又点是棱的中点，

所以EO是的中位线，

所以EO// PC

因为EO平面，平面，

所以PC//平面BDE；

（Ⅱ）证明：(法一）在和中，

因为，，，

所以≌，又点是棱的中点，

所以，

所以

因为平面 平面，平面 平面，

平面

所以平面，

所以EO⊥AC,EO⊥BD,

因为EO//PC

所以PC⊥AC,PC⊥BD,又AC∩BD=O

所以PC⊥平面ABCD．

（法二）连接PO

因为底面ABCD是正方形，

所以O是BD的中点，BD⊥AC,又PB=PD,

所以PO⊥BD,又PO∩AC=O,PO平面PAC,AC平面PAC

所以BD⊥平面PAC

又OE平面PAC, 所以BD⊥OE，

因为平面 平面，平面 平面，

平面

所以平面，

所以EO⊥AC,EO⊥BD,

因为OE∥PC,

所以PC⊥AC,PC⊥BD,又AC∩BD=O

所以所以PC⊥平面ABCD．

(Ⅲ) 不能成立