题目内容
已知双曲线C: -
- =1(a>0,b>0)的离心率e=
=1(a>0,b>0)的离心率e= ,且2a2=3c,若双曲线C上的点P满足
,且2a2=3c,若双曲线C上的点P满足
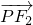 =1,则|
=1,则| |
| |=
|=
- A.5
- B.4
- C.3
- D.2
C
分析:先确定双曲线中的几何量,再利用数量积的定义,余弦定理及双曲线的定义,即可求得结论.
解答:∵双曲线的离心率e= ,∴
,∴ =
=
∵2a2=3c,∴a= ,c=2
,c=2
不妨设P再双曲线的右支上, 、
、 的夹角为α,|
的夹角为α,| |=m、
|=m、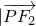 |=n,则
|=n,则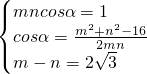
整理得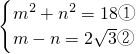 ,①2-②得2mn=18-12
,①2-②得2mn=18-12
∴mn=3,即| |
| |=3
|=3
故选C.
点评:本题考查双曲线的标准方程,考查数量积的定义,余弦定理及双曲线的定义,考查学生的计算能力,属于中档题.
分析:先确定双曲线中的几何量,再利用数量积的定义,余弦定理及双曲线的定义,即可求得结论.
解答:∵双曲线的离心率e=
 ,∴
,∴ =
=
∵2a2=3c,∴a=
 ,c=2
,c=2不妨设P再双曲线的右支上,
 、
、 的夹角为α,|
的夹角为α,| |=m、
|=m、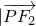 |=n,则
|=n,则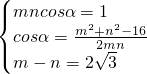
整理得
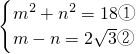 ,①2-②得2mn=18-12
,①2-②得2mn=18-12∴mn=3,即|
 |
| |=3
|=3故选C.
点评:本题考查双曲线的标准方程,考查数量积的定义,余弦定理及双曲线的定义,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ,右准线方程为x=
,右准线方程为x=
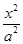 -
- =1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为(
)
=1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为(
) -
-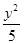 =1
B.
=1
B.  -
- =1 C.
=1 C.  -
- =1
=1 -
- =1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为
=1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为 -
- =1 B、
=1 B、 -
- =1
C、
=1
C、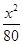 -
- =1[w~#
=1[w~#