题目内容
由约束条件 确定的可行域D能被半径为
确定的可行域D能被半径为 的圆面完全覆盖,则实数K的取值范围是________.
的圆面完全覆盖,则实数K的取值范围是________.
K≤-
分析:由可行域能被圆覆盖得到可行域是封闭的,判断出k<0;画出可行域,令可行域最长的边小于等于直径即可.
列出不等式求出k的范围.
解答:∵可行域能被圆覆盖,
∴可行域是封闭的,
∴k<0,
作出可行域:

结合图,要使可行域能被 为半径的圆覆盖,
为半径的圆覆盖,
只需 ,
,
解得 ,
,
故答案为: .
.
点评:本题考查画不等式组表示的平面区域、考查将图形的大小关系转化为不等式.

分析:由可行域能被圆覆盖得到可行域是封闭的,判断出k<0;画出可行域,令可行域最长的边小于等于直径即可.
列出不等式求出k的范围.
解答:∵可行域能被圆覆盖,
∴可行域是封闭的,
∴k<0,
作出可行域:

结合图,要使可行域能被
 为半径的圆覆盖,
为半径的圆覆盖,只需
 ,
,解得
 ,
,故答案为:
 .
.点评:本题考查画不等式组表示的平面区域、考查将图形的大小关系转化为不等式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 确定的可行域D能被半径为1的圆面完全覆盖,则实数
确定的可行域D能被半径为1的圆面完全覆盖,则实数 的取值范围是
。
的取值范围是
。 确定的可行域D能被半径为1的圆面完全覆盖,则实数
确定的可行域D能被半径为1的圆面完全覆盖,则实数 的取值范围是__________.
的取值范围是__________.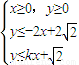 确定的可行域D能被半径为1的圆面完全覆盖,则实数k的取值范围是 .
确定的可行域D能被半径为1的圆面完全覆盖,则实数k的取值范围是 .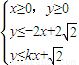 确定的可行域D能被半径为1的圆面完全覆盖,则实数k的取值范围是 .
确定的可行域D能被半径为1的圆面完全覆盖,则实数k的取值范围是 .