题目内容
一个四棱锥P-ABCD的正视图是边长为2的正方形及其一条对角线，侧视图和俯视图全全等的等腰直角三角形，直角边长为2，直观图如图．
（1）求四棱锥P-ABCD的体积：
（2）求直线PC和面PAB所成线面角的余弦值；
（3）M为棱PB上的一点，当PM长为何值时，CM⊥PA?
（1）VP-ABCD=
SABCD·PD=
（2）以D为坐标原点，建立 设
为平面PAB的法向量
，PC与
所成角
，有
，PC与PAB所成角为
∴余弦值为
（3）由M在棱PB上，
，得M（
）
即当|PM|=
|PB|=
时
CM⊥PA
练习册系列答案
金状元绩优好卷系列答案
相关题目
侧棱长为a的正三棱锥P-ABC的侧面都是直角三角形，且四个顶点都在一个球面上，则该球的表面积为（ ）
A、
| ||
| B、2πa2 | ||
C、
| ||
| D、3πa2 |
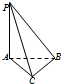已知如图在三棱锥P-ABC中，PA⊥平面ABC，AC⊥BC，PA=AC=BC=1，若三棱锥P-ABC的四个顶点都在某一个球面上，则该球的表面积为（ ）