题目内容
已知
=(2asin2x,a),
=(-1,2
sinxcosx+1),O为坐标原点,a≠0,设f(x)=
•
+b,b>a.
(I)若a>0,写出函数y=f(x)的单调递增区间;
(II)若函数y=f(x)的定义域为[
,π],值域为[2,5],求实数a与b的值.
| OA |
| OB |
| 3 |
| OA |
| OB |
(I)若a>0,写出函数y=f(x)的单调递增区间;
(II)若函数y=f(x)的定义域为[
| π |
| 2 |
(I)f(x)=-2asin2x+2
asinxcosx+a+b=2asin(2x+
)+b
∵a>0,∴由2kπ-
≤2x+
≤2kπ+
得函数y=f(x)的单调递增区间是[kπ-
,kπ+
](k∈Z)
(写成[kπ+
,kπ+
](k∈Z)也可以)
(II)x∈[
,π]时,2x+
∈[
,
],sin(2x+
)∈[-1,
]
当a>0时,f(x)∈[-2a+b,a+b]∴
,得
,
当a<0时,f(x)∈[a+b,-2a+b]∴
,得
| 3 |
| π |
| 6 |
∵a>0,∴由2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
得函数y=f(x)的单调递增区间是[kπ-
| π |
| 3 |
| π |
| 6 |
(写成[kπ+
| 2π |
| 3 |
| 7π |
| 6 |
(II)x∈[
| π |
| 2 |
| π |
| 6 |
| 7π |
| 6 |
| 13π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
当a>0时,f(x)∈[-2a+b,a+b]∴
|
|
当a<0时,f(x)∈[a+b,-2a+b]∴
|
|

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 ,求
,求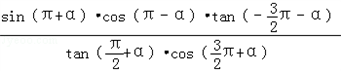 的值.
的值. ,则sinα·cosα=
,则sinα·cosα= 

 或-
或-

 的结果是
的结果是 ,其中m、n、
,其中m、n、 、
、 都是非零实数,若
都是非零实数,若 ,则
,则 =( )。
=( )。