题目内容
四棱锥 的底面是矩形,锥顶点在底面的射影是矩形对角线的交点,四棱锥及其三视图如下(AB平行于主视图投影平面)
的底面是矩形,锥顶点在底面的射影是矩形对角线的交点,四棱锥及其三视图如下(AB平行于主视图投影平面)
则四棱锥 的体积=( )
的体积=( )
| A.24 | B.18 | C. | D.8 |
D
解析试题分析:由三视图可知四棱锥的底面矩形的两边长分别为4和2,高为3,因此 .
.
考点:三视图与体积.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
若圆柱的底面直径和高都与球的直径相等,圆柱、球的表面积分别记为 、
、 ,则
,则 :
: =( ).
=( ).
| A.1:1 | B.2:1 | C.3:2 | D.4:1 |
一个几何体的正视图、侧视图、和俯视图形状都相同,大小均相等,则这个几何体不可以是( )
| A.球 | B.三棱锥 | C.正方体 | D.圆柱 |
平面 截球O的球面所得圆的半径为1,球心O到平面α的距离为
截球O的球面所得圆的半径为1,球心O到平面α的距离为 ,则此球的体积为( )
,则此球的体积为( )
A. π π | B.4 π π | C.4 π π | D.6 π π |
已知正方体的棱长为1,则该正方体外接球的体积为( )
A. | B. | C. | D. |
右图是棱长为2的正方体的表面展开图,则多面体 的体积为( )
的体积为( )
| A.2 | B. | C. | D. |
已知三棱锥的三视图如图所示,则它的外接球表面积为( )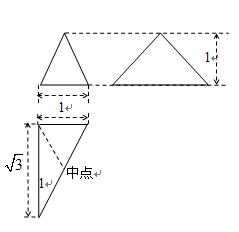
A. |
B.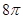 |
C.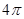 |
D.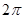 |
 为( ).
为( ).





