选做题已知矩阵A=,A的一个特征值λ=2.其对应的特征向量是α1=.(1)求矩阵A,(2)若向量β=.计算A5β的值. 题目和参考答案——青夏教育精英家教网—

题目内容

选做题已知矩阵A=,A的一个特征值λ=2，其对应的特征向量是α₁=.

（1）求矩阵A；

（2）若向量β=，计算A⁵β的值.

解：(1)A=；

(2)矩阵A的特征多项式为f(λ)==λ²-5λ+6=0，

得λ₁=2,λ₂=3,

当λ₁=2时,α₁=,当λ₂=3时,得α₂=.

由β=mα₁+nα₂，得得m=3,n=1.

∴A⁵β=A⁵(3α₁+α₂)=3(A⁵α₁)+A⁵α₂

=3(λ₁⁵α₁)+λ₂⁵α₂=3×2⁵+3⁵=.

练习册系列答案

小学生10分钟口算测试100分系列答案

3	3
c	d

，若矩阵A属于特征值6的一个特征向量为

，属于特征值1的一个特征向量为

&-2；
（Ⅰ）求矩阵A；
（Ⅱ）判断矩阵A是否可逆，若可逆求出其逆矩阵A^-1．
（2）选修4-4：坐标系与参数方程
已知直线的极坐标方程为ρsin(θ+

，圆M的参数方程为

x=2cosθ

y=-2+2sinθ

（其中θ为参数）．
（Ⅰ）将直线的极坐标方程化为直角坐标方程；
（Ⅱ）求圆M上的点到直线的距离的最小值．
（3）选修4-5：不等式选讲，设函数f（x）=|x-1|+|x-a|；
（Ⅰ）若a=-1，解不等式f（x）≥3；
（Ⅱ）如果关于x的不等式f（x）≤2有解，求a的取值范围．

矩阵与变换选做题

已知矩阵A＝有一个属于特征值1的特征向量．

(Ⅰ)求矩阵A；

(Ⅱ)矩阵B＝，点O(0，0)，M(2，－1)，N(0，2)，求ΔOMN在矩阵AB的对应变换作用下所得到的Δ的面积．

本题有(1)．(2)．(3)三个选做题，每题7分，请考生任选2题作答，满分14分．如果多做，则按所做的前两题计分．作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中．

（1）(本小题满分7分)选修4－2：矩阵与变换选做题

已知矩阵A=有一个属于特征值1的特征向量.

(Ⅰ) 求矩阵A；

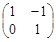(Ⅱ) 矩阵B=，点O(0,0)，M(2，-1)，N(0，2)，求在矩阵AB的对应变换作用下所得到的的面积.

（2）(本小题满分7分)选修4－4：坐标系与参数方程选做题

在直角坐标平面内，以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系.已知曲线的参数方程为，曲线的极坐标方程为．

（Ⅰ）将曲线的参数方程化为普通方程；（Ⅱ）判断曲线与曲线的交点个数，并说明理由．

（3）(本小题满分7分)选修4－5：不等式选讲选做题

已知函数，不等式在上恒成立．

（Ⅰ）求的取值范围；

（Ⅱ）记的最大值为，若正实数满足，求的最大值．

选做题
已知矩阵A=

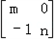．在平面直角坐标系中，设直线l：2x+y﹣7=0在矩阵A对应的变换作用下得到另一直线l′：9x+y﹣91=0，求实数m、n的值．

试题分类