题目内容
自原点O做圆(x-1)2+y2=1的不重合两弦OA,OB若|OA|•|OB|=k(定值),那么不论A,B两点位置怎样,直线AB恒切与一个定圆,并求出定圆方程.
解:由题意,圆(x-1)2+y2=1是△AOB 的外接圆,半径为1,根据正弦定理:|AB|=2Rsin∠AOB=2sin∠AOB
设AB边上的高为h,则△AOB的面积S= |AB|•h=h•sin∠AOB
|AB|•h=h•sin∠AOB
∵S= |OA|•|OB|•sin∠AOB=
|OA|•|OB|•sin∠AOB= ksin∠AOB
ksin∠AOB
∴h= 为定值
为定值
即O到AB的距离为定值
∴直线AB与以原点为圆心, 为半径的圆相切,圆的方程为x2+y2=
为半径的圆相切,圆的方程为x2+y2=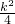 .
.
分析:设AB边上的高为h,则△AOB的面积S= |AB|•h,再利用S=
|AB|•h,再利用S= |OA|•|OB|•sin∠AOB,即可得到结论.
|OA|•|OB|•sin∠AOB,即可得到结论.
点评:本题考查直线与圆的位置关系,考查圆的方程,考查学生的计算能力,属于基础题.
设AB边上的高为h,则△AOB的面积S=
 |AB|•h=h•sin∠AOB
|AB|•h=h•sin∠AOB∵S=
 |OA|•|OB|•sin∠AOB=
|OA|•|OB|•sin∠AOB= ksin∠AOB
ksin∠AOB∴h=
 为定值
为定值即O到AB的距离为定值

∴直线AB与以原点为圆心,
 为半径的圆相切,圆的方程为x2+y2=
为半径的圆相切,圆的方程为x2+y2=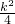 .
.分析:设AB边上的高为h,则△AOB的面积S=
 |AB|•h,再利用S=
|AB|•h,再利用S= |OA|•|OB|•sin∠AOB,即可得到结论.
|OA|•|OB|•sin∠AOB,即可得到结论.点评:本题考查直线与圆的位置关系,考查圆的方程,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
 选做题本题包括A,B,C,D四小题,请选定其中 两题 作答,每小题10分,共计20分,
选做题本题包括A,B,C,D四小题,请选定其中 两题 作答,每小题10分,共计20分,