题目内容
求倾斜角是45°,并且与原点的距离是5的直线的方程.分析:求出倾斜角是45°的直线的斜率,设出直线方程,利用原点与直线的距离为5,求出直线方程中的未知数,即可确定直线方程.
解答:解:因直线斜率为tan45°=1,可设直线方程y=x+b,化为一般式x-y+b=0,
由直线与原点距离是5,得
=5?|b|=5
∴b=±5
,
所以直线方程为x-y+5
=0,或y-5
=0.
由直线与原点距离是5,得
| |0-0+b| | ||
|
| 2 |
| 2 |
所以直线方程为x-y+5
| 2 |
| 2 |
点评:本题考查点到直线的距离公式,考查计算能力,是基础题.

练习册系列答案
相关题目
 ]在区间(t,3)上总不是单调函数,求m的取值范围;
]在区间(t,3)上总不是单调函数,求m的取值范围;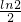 ×
× ×
×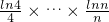 与
与 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.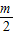 ]在区间(t,3)上总不是单调函数,求m的取值范围;
]在区间(t,3)上总不是单调函数,求m的取值范围; ×
×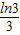 ×
×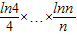 与
与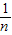 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.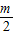 ]在区间(t,3)上总不是单调函数,求m的取值范围;
]在区间(t,3)上总不是单调函数,求m的取值范围;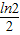 ×
×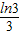 ×
×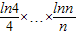 与
与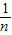 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.