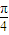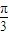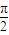题目内容
若直线x= 被曲线C:(x-arcsina)(x-arccosa)+(y-arcsina)(y+arccosa)=0所截的弦长为d,当a变化时d的最小值是
被曲线C:(x-arcsina)(x-arccosa)+(y-arcsina)(y+arccosa)=0所截的弦长为d,当a变化时d的最小值是
- A.

- B.

- C.

- D.π
C
分析:将方程化为标准方程,求得圆心到直线的距离,进而可计算弦长,再利用配方法,即可求得结论.
解答:曲线C:(x-arcsina)(x-arccosa)+(y-arcsina)(y+arccosa)=0可化为(x- )2+(y-
)2+(y- )2=
)2=
∴圆心到直线的距离为| -
- |
|
∴ d2=
d2= -(
-( -
- )2=(
)2=( )2+
)2+ ×
× -
-
设arcsina=α,则arccosa=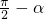 ,
,
∴ d2=(α-
d2=(α- )2+
)2+
∴ 时,
时, d2取得最小值
d2取得最小值
∴当a变化时d的最小值是
故选C.
点评:本题考查直线与圆的位置关系,考查弦长的计算,考查学生的计算能力,属于中档题.
分析:将方程化为标准方程,求得圆心到直线的距离,进而可计算弦长,再利用配方法,即可求得结论.
解答:曲线C:(x-arcsina)(x-arccosa)+(y-arcsina)(y+arccosa)=0可化为(x-
 )2+(y-
)2+(y- )2=
)2=
∴圆心到直线的距离为|
 -
- |
|∴
 d2=
d2= -(
-( -
- )2=(
)2=( )2+
)2+ ×
× -
-
设arcsina=α,则arccosa=
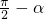 ,
,∴
 d2=(α-
d2=(α- )2+
)2+
∴
 时,
时, d2取得最小值
d2取得最小值
∴当a变化时d的最小值是

故选C.
点评:本题考查直线与圆的位置关系,考查弦长的计算,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
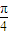 被曲线C:(x-arcsina)(x-arccosa)+(y-arcsina)(y+arccosa)=0所截的弦长为d,当a变化时d的最小值是( )
被曲线C:(x-arcsina)(x-arccosa)+(y-arcsina)(y+arccosa)=0所截的弦长为d,当a变化时d的最小值是( )