题目内容
若不等式（-1）na＜2+
对任意n∈N*恒成立，则实数a的取值范围是
- A.[-2，
） - B.（-2，）
- C.[-3，）
- D.（-3，）
A
分析：对n进行分类讨论，分离出参数a，将原问题转化为求函数的最小值问题解决．
解答：当n为正偶数时，
a＜2-
恒成立，又2-为增函数，其最小值为2-
=
∴a＜．
当n为正奇数时，-a＜2+，即a＞-2-恒成立．
而-2-为增函数，对任意的正整数n，有-2-＜-2，
∴a≥-2．
故a∈[-2，）．
点评：本题主要考查了不等式的证明及恒成立问题，属于基础题．
分析：对n进行分类讨论，分离出参数a，将原问题转化为求函数的最小值问题解决．
解答：当n为正偶数时，
a＜2-
恒成立，又2-为增函数，其最小值为2-=∴a＜
．当n为正奇数时，-a＜2+
，即a＞-2-恒成立．而-2-
为增函数，对任意的正整数n，有-2-＜-2，∴a≥-2．
故a∈[-2，
）．点评：本题主要考查了不等式的证明及恒成立问题，属于基础题．
练习册系列答案
相关题目
若不等式（-1）na＜2+
对任意n∈N*恒成立，则实数a的取值范围是（ ）
| (-1)n+1 |
| n |
A、[-2，
| ||
B、（-2，
| ||
C、[-3，
| ||
D、（-3，
|
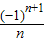对任意n∈N*恒成立，则实数a的取值范围是（ ）
）
）
）
）
对任意n∈N*恒成立，则实数a的取值范围是（ ）
）
）
）
）
对任意n∈N*恒成立，则实数a的取值范围是（ ）
）
）
）
）
对任意n∈N*恒成立，则实数a的取值范围是（ ）
）
）
）
）