题目内容
在△ABC中，已知角A、B、C所对的三边分别是a，b，c，且b2=ac
（1）求证：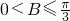
；
（2）求函数
的值域．
解：（1）cosB=
∴
（2）
∴
分析：（1）利用余弦定理表示出cosB，进而利用基本不等式求得cosB的范围，则B的范围可得．
（2）利用同角三角函数的基本关系把1+sin2B整理成（sinB+cosB）2，进而利用两角和公式整理后，利用正弦函数和B的范围求得函数的值域．
点评：本题考查余弦定理，和角公式以及三角函数值域求法．考查了基础知识的应用．
∴（2）
∴
分析：（1）利用余弦定理表示出cosB，进而利用基本不等式求得cosB的范围，则B的范围可得．
（2）利用同角三角函数的基本关系把1+sin2B整理成（sinB+cosB）2，进而利用两角和公式整理后，利用正弦函数和B的范围求得函数的值域．
点评：本题考查余弦定理，和角公式以及三角函数值域求法．考查了基础知识的应用．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目