题目内容
已知函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ,
,![]() ,
,![]() 是函数
是函数![]() 图像上的两点,且线段
图像上的两点,且线段![]() 的中点P的横坐标为
的中点P的横坐标为![]() .
.
(1)求证:点P的纵坐标是定值;
(2)若数列![]() 的通项公式为
的通项公式为![]() , 求数列
, 求数列![]() 的前m项和
的前m项和![]() ;
;
(3)设数列![]() 满足:
满足:![]() ,设
,设![]() ,
,
若(2)中的![]() 满足对任意不小于2的正整数n,
满足对任意不小于2的正整数n, ![]() 恒成立, 试求m的最大值.
恒成立, 试求m的最大值.
解:(1)当![]() 时,
时,![]() 在
在![]() 上单调递减,又
上单调递减,又![]() 的最小值为
的最小值为![]() ,
,
∴![]() ,得t=1 ;
,得t=1 ;
当![]() 时,
时,![]() 在
在![]() 上单调递增,又
上单调递增,又![]() 的最小值为
的最小值为![]() ,
,
∴![]() ,得t=2(舍) ;
,得t=2(舍) ;
当t = 0时,![]() (舍),
(舍),
∴t = 1, ![]() .
.
∵![]() ∴
∴![]() ,
,
∴![]() ,即p点的纵坐标为定值
,即p点的纵坐标为定值![]() 。
。
(2)由(1)可知, ![]() , 所以
, 所以![]() ,
,
即![]()
由![]() , … ①
, … ①
得![]() …②
…②
由①+②, 得![]()
∴![]()
(3) ∵![]()
![]() , ……③
, ……③
∴对任意的![]() . ……④
. ……④
由③、④, 得![]() 即
即![]() .
.
∴![]() .
.
∵![]()
∴数列![]() 是单调递增数列.
是单调递增数列.
∴![]() 关于n递增. 当
关于n递增. 当![]() , 且
, 且![]() 时,
时, ![]() .
.
∵![]()
∴![]() ∴
∴![]() 即
即![]()
∴![]() ∴m的最大值为6.
∴m的最大值为6.

练习册系列答案
相关题目
 在
在 上的最大值是3,最小值是2,则实数
上的最大值是3,最小值是2,则实数 的取值范围是
.
的取值范围是
.
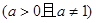 在
在 上的最大值与最小值之和为
上的最大值与最小值之和为 ,记
,记 。
。 的值;
的值; ;
; 的值
的值 在
在
 上的最大值是3,最小值是2,则实数
上的最大值是3,最小值是2,则实数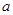 的取值范围是
.
的取值范围是
.