题目内容
设F1、F2分别是椭圆 的左、右焦点,过F1的直线?与E相交于A、B两点,且|AF2|,|AB|,|BF2|成等差数列,则|AB|的长为
的左、右焦点,过F1的直线?与E相交于A、B两点,且|AF2|,|AB|,|BF2|成等差数列,则|AB|的长为
- A.

- B.1
- C.

- D.

C
分析:利用等差数列的性质,结合椭圆的定义,即可求得|AB|.
解答:∵|AF2|,|AB|,|BF2|成等差数列,
∴|AF2|+|BF2|=2|AB|,
∵|AF2|+|AB|+|BF2|=4a=4
∴3|AB|=4
∴|AB|=
故选C.
点评:本题考查椭圆的定义,考查等差数列的性质,考查计算能力,属于基础题.
分析:利用等差数列的性质,结合椭圆的定义,即可求得|AB|.
解答:∵|AF2|,|AB|,|BF2|成等差数列,
∴|AF2|+|BF2|=2|AB|,
∵|AF2|+|AB|+|BF2|=4a=4
∴3|AB|=4
∴|AB|=

故选C.
点评:本题考查椭圆的定义,考查等差数列的性质,考查计算能力,属于基础题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 的左、右焦点,其右焦点是直线y=x-1与x轴的交点,短轴的长是焦距的2倍.
的左、右焦点,其右焦点是直线y=x-1与x轴的交点,短轴的长是焦距的2倍. 的最大值和最小值;
的最大值和最小值; 的左、右焦点,P为椭圆上任一点,点M的坐标为(6,4),则
的左、右焦点,P为椭圆上任一点,点M的坐标为(6,4),则 的最大值为__________.
的最大值为__________.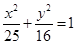 的左、右焦点,P为椭圆上任一点,点M的坐标为(6,4),则|PM|+|PF1|的最大值为_______
的左、右焦点,P为椭圆上任一点,点M的坐标为(6,4),则|PM|+|PF1|的最大值为_______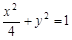 的左、右焦点,P是第一象限内该椭圆上的一点,且
的左、右焦点,P是第一象限内该椭圆上的一点,且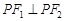 ,求点P的横坐标为( )
,求点P的横坐标为( )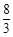 C.
C. D.
D.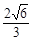
 的左、右焦点。
的左、右焦点。 ,求点P的坐标;
,求点P的坐标;