题目内容

已知A、B是三角形的内角，且（1+tanA）（1+tanB）=2，则A+B=______．
（1+tanA）（1+tanB）=tanAtanB+（tanA+tanB）+1=2
∴tanA+tanB=1-tanAtanB
∴tan（A+B）=
tanA+tanB
1-tanAtanB
=1
∵A、B是三角形的内角
∴A+B=
π
4

故答案为
π
4
练习册系列答案
相关题目
已知A，B是△ABC的两个内角，
a
=
2
cos
A+B
2
i
+sin
A-B
2
j
（其中
i
，
j
是互相垂直的单位向量），若|
a
|=
6
2
．
（1）试问tanA•tanB是否为定值，若是定值，请求出，否则说明理由；
（2）求tanC的最大值，并判断此时三角形的形状．
已知A、B是三角形的内角，且（1+tanA）（1+tanB）=2，则A+B=
 
．
已知A，B是△ABC的两个内角，
a
=
2
cos
A+B
2
i
+sin
A-B
2
j
，（其中
i
，
j
是互相垂直的单位向量），若|
a
|=
6
2
．
（1）试问tanA•tanB是否为定值，若是定值，请求出，否则请说明理由；
（2）求tanC的最大值，并判断此时三角形的形状．


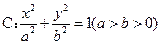已知A，B是椭圆的左，右顶点，，过椭圆C的右焦点F的直线交椭圆于点M，N，交直线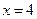于点P，且直线PA，PF，PB的斜率成等差数列,R和Q是椭圆上的两动点，R和Q的横坐标之和为2，RQ的中垂线交X轴于T点

(1)求椭圆C的方程；
（2）求三角形MNT的面积的最大值

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网