题目内容
 如图,在正方体ABCD-A1B1C1D1中,若E为A1C1与B1D1的交点,F为DD1的中点,则直线EF与直线BC所成角的大小为________(用反三角函数值表示).
如图,在正方体ABCD-A1B1C1D1中,若E为A1C1与B1D1的交点,F为DD1的中点,则直线EF与直线BC所成角的大小为________(用反三角函数值表示).
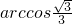
分析:设正方体ABCD-A1B1C1D1的棱长为2,以AB为x轴,AD为y轴,AA1为z轴,建立空间直角坐标系,则
 ,
, ,设直线EF与直线BC所成角为α,则
,设直线EF与直线BC所成角为α,则 =|
=| |=
|= ,由此能求出直线EF与直线BC所成角的大小.
,由此能求出直线EF与直线BC所成角的大小.解答:设正方体ABCD-A1B1C1D1的棱长为2,以AB为x轴,AD为y轴,AA1为z轴,建立空间直角坐标系,
则B(1,0,0),C(1,1,0),
 ,
,E(1,1,2),F(0,2,1),
 ,
,设直线EF与直线BC所成角为α,
则

=|
 |
|=
 ,
,∴α=
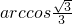 .
.故答案为:
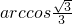 .
.点评:本题考查两条异面直线所成角的大小,解题时要认真审题,合理地建立空间直角坐标系,利用向量法求解两条异面直线所成角的大小.

练习册系列答案
相关题目
 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记
如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点,
如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点, 如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为( )
如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为( )