题目内容
7.已知函数f(x)=$\sqrt{3}$cos2x-2cos2(x+$\frac{π}{4}$)+1.(Ⅰ)求f(x)的单调递增区间;
(Ⅱ)求f(x)在区间[0,$\frac{π}{2}$]上的最值.
分析 (Ⅰ)化函数f(x)为正弦型函数,
根据正弦函数的单调性求出f(x)的单调递增区间;
(Ⅱ)求出x∈[0,$\frac{π}{2}$]时,sin(2x+$\frac{π}{3}$)的取值范围,
即可求出f(x)的最大、最小值.
解答 解:(Ⅰ)函数f(x)=$\sqrt{3}$cos2x-2cos2(x+$\frac{π}{4}$)+1
=$\sqrt{3}$cos2x-cos(2x+$\frac{π}{2}$)
=$\sqrt{3}$cos2x+sin2x
=2sin(2x+$\frac{π}{3}$);
令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,k∈Z,
解得kπ-$\frac{5π}{12}$≤x≤kπ+$\frac{π}{12}$,k∈Z,
∴f(x)的单调递增区间为[kπ-$\frac{5π}{12}$,kπ+$\frac{π}{12}$](k∈Z);
(Ⅱ)当x∈[0,$\frac{π}{2}$]时,2x+$\frac{π}{3}$∈[$\frac{π}{3}$,$\frac{4π}{3}$],
∴sin(2x+$\frac{π}{3}$)∈[-$\frac{\sqrt{3}}{2}$,1],
∴f(x)在区间[0,$\frac{π}{2}$]上的最大值为2,最小值为-$\sqrt{3}$;
且x=$\frac{π}{12}$时f(x)取得最大值2,x=$\frac{π}{2}$时f(x)取得最小值-$\sqrt{3}$.
点评 本题考查了三角函数的恒等变换与三角函数的图象和性质的应用问题,是中档题.

练习册系列答案
相关题目
17.已知F1,F2是椭圆和双曲线的公共焦点,P是它们的一个公共点,且$∠{F_1}P{F_2}=\frac{π}{3}$,则椭圆和双曲线离心率倒数之和的最大值为( )
| A. | $\frac{4}{3}$ | B. | $\frac{{4\sqrt{3}}}{3}$ | C. | 4 | D. | $\frac{{4\sqrt{6}}}{3}$ |
2.设(1+x)6=a0+a1x+a2x2+…+a6x6,其中x、ai∈R,i=0,1,…,6,则a1+a3+a5=( )
| A. | 16 | B. | 32 | C. | 64 | D. | 128 |
12.已知实数x、y满足$\left\{\begin{array}{l}{x-4y≤-3}\\{3x+5y≤25}\\{x≥1}\end{array}\right.$,则z=x-y的取值范围是( )
| A. | [0,3] | B. | [-$\frac{17}{5}$,3] | C. | [-$\frac{17}{5}$,1] | D. | [-$\frac{17}{5}$,0] |
3.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积是( )
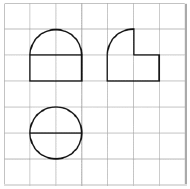

| A. | $\frac{7π}{2}$ | B. | 4π | C. | $\frac{9π}{2}$ | D. | 5π |
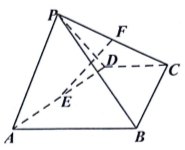 如图,在四棱锥P-ABCD中,△PAD为正三角形,四边形ABCD为直角梯形,CD∥AB,BC⊥AB,平面PAD⊥平面ABCD,点E、F分别为AD、CP的中点,AD=AB=2CD=2.
如图,在四棱锥P-ABCD中,△PAD为正三角形,四边形ABCD为直角梯形,CD∥AB,BC⊥AB,平面PAD⊥平面ABCD,点E、F分别为AD、CP的中点,AD=AB=2CD=2.