题目内容
 如图1,在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=
如图1,在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC= ,D是AP的中点,E,F,G分别为PC、PD、CB的中点,将△PCD沿CD折起,使得PD⊥平面ABCD,如图2.
,D是AP的中点,E,F,G分别为PC、PD、CB的中点,将△PCD沿CD折起,使得PD⊥平面ABCD,如图2.
(Ⅰ)求三棱椎D-PAB的体积;
(Ⅱ) 求证:AP∥平面EFG;
(Ⅲ)求二面角G-EF-D的大小.
 解:(Ⅰ)
解:(Ⅰ) .
.(Ⅱ)证明:如图以D为原点,以
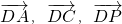 为方向向量建立空间直角坐标系D-xyz.
为方向向量建立空间直角坐标系D-xyz.则有关点及向量的坐标为:


设平面EFG的法向量为
 ∴
∴ .取
.取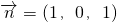 .
.∵
 ,∴
,∴ ,
,又AP?平面EFG.∴AP∥平面EFG
(Ⅲ)由已知底面ABCD是正方形∴AD⊥DC,又∵PD⊥面ABCD∴AD⊥PD
又PD∩CD=D∴AD⊥平面PCD,∴向量
 是平面PCD的一个法向量,
是平面PCD的一个法向量, =(2,0,0)
=(2,0,0)平面EFG的法向量为
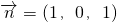 ∴
∴ .
.结合图知二面角G-EF-D的平面角为450.
分析:(I)根据要求的三棱锥的体积与已知底面和高的三棱锥的体积相等,写出体积的表示式,得到结果.
(II)建立坐标系,写出要用的点的坐标,进而写出向量,设出平面的法向量,求出法向量,根据法向量与直线的方向向量垂直,得到线面平行.
(III)两个平面的法向量一个已经求出,另一个在图形中存在,这样根据两个平面的法向量所成的角,得到两个平面的二面角.
点评:本题考查立体几何的综合题目,本题解题的关键是建立坐标系,把一些理论性的正明转化成运算,降低了题目的难度.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目


 (2013•海淀区二模)如图1,在直角梯形ABCD中,∠ABC=∠DAB=90°,∠CAB=30°,BC=2,AD=4.把△DAC沿对角线AC折起到△PAC的位置,如图2所示,使得点P在平面ABC上的正投影H恰好落在线段AC上,连接PB,点E,F分别为线段PA,PB的中点.
(2013•海淀区二模)如图1,在直角梯形ABCD中,∠ABC=∠DAB=90°,∠CAB=30°,BC=2,AD=4.把△DAC沿对角线AC折起到△PAC的位置,如图2所示,使得点P在平面ABC上的正投影H恰好落在线段AC上,连接PB,点E,F分别为线段PA,PB的中点.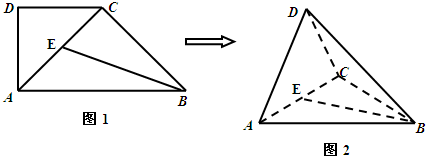 (1)求证:DA⊥BC;
(1)求证:DA⊥BC;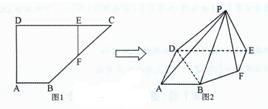 如图1,在直角梯形ABCD中,AB∥CD,∠A=90°,AB=2,CD=6,AD=3,E为CD上一点,且DE=4,过E作EF∥AD交BC于F现将△CEF沿EF折起到△PEF,使∠PED=60°,如图2.
如图1,在直角梯形ABCD中,AB∥CD,∠A=90°,AB=2,CD=6,AD=3,E为CD上一点,且DE=4,过E作EF∥AD交BC于F现将△CEF沿EF折起到△PEF,使∠PED=60°,如图2.