题目内容
(本小题满分l2分)(注意:在试题卷上作答无效)
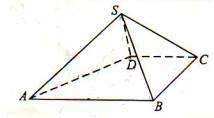 如图,四棱锥
如图,四棱锥![]() 中,
中, ![]() ,
,![]() ,侧面
,侧面![]() 为等边三角形,
为等边三角形,
![]() .
.
(I)证明:![]() 平面SAB;
平面SAB;
(II)求AB与平面SBC所成的角的大小。
解法一:
(I)取AB中点E,连结DE,则四边形BCDE为矩形,DE=CB=2,
连结SE,则![]()
又SD=1,故![]() ,
,
所以![]() 为直角。 …………3分
为直角。 …………3分
由![]() ,
,
得![]() 平面SDE,所以
平面SDE,所以![]() 。
。
SD与两条相交直线AB、SE都垂直。
所以![]() 平面SAB。 …………6分
平面SAB。 …………6分
(II)由![]() 平面SDE知,
平面SDE知,
平面![]() 平面SED。
平面SED。
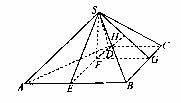 作
作![]() 垂足为F,则SF
垂足为F,则SF![]() 平面ABCD,
平面ABCD,
![]()
作![]() ,垂足为G,则FG=DC=1。
,垂足为G,则FG=DC=1。
连结SG,则![]() ,
,
又![]() ,
,
故![]() 平面SFG,平面SBC
平面SFG,平面SBC![]() 平面SFG。 …………9分
平面SFG。 …………9分
作![]() ,H为垂足,则
,H为垂足,则![]() 平面SBC。
平面SBC。
![]() ,即F到平面SBC的距离为
,即F到平面SBC的距离为![]()
由于ED//BC,所以ED//平面SBC,E到平面SBC的距离d也有![]()
设AB与平面SBC所成的角为α,
则![]() …………12分
…………12分
解法二:
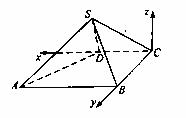
以C为坐标原点,射线CD为x轴正半轴,建立如图所示的空间直角坐标系C—xyz。
设D(1,0,0),则A(2,2,0)、B(0,2,0)。
又设![]()
(I)![]() ,
,![]() ,
,
 由
由![]() 得
得
![]()
故x=1。
由![]()
又由![]()
即![]() …………3分
…………3分
于是![]() ,
,
![]()
故![]()
所以![]() 平面SAB。
平面SAB。
(II)设平面SBC的法向量![]() ,
,
则![]()
又![]()
故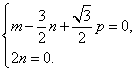 …………9分
…………9分
取p=2得![]() 。
。
![]()
故AB与平面SBC所成的角为![]()

练习册系列答案
相关题目
 ,bn+1=-
,bn+1=- Sn(n∈N*).
Sn(n∈N*). +
+ +…+
+…+ ,求Tn的表达式
,求Tn的表达式 ,过左焦点
,过左焦点 作直线
作直线 与椭圆交于点P,Q,直线AP,AQ分别与直线
与椭圆交于点P,Q,直线AP,AQ分别与直线 交于点
交于点 .
. 为直径的圆经过焦点
为直径的圆经过焦点 .
. :函数
:函数 (
( )的值域是
)的值域是 ;命题
;命题 :指数函数
:指数函数 在
在 上是减函数.若命题“
上是减函数.若命题“ 的范围.
的范围. 并且与曲线
并且与曲线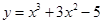 相切的直线方程.
相切的直线方程.