题目内容
如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是圆O的直径,上底CD的端点在圆周上.(1)求梯形ABCD的周长y与腰长x间的函数解析式,并求出它的定义域;
(2)求梯形ABCD的周长y的最大值.

【答案】分析:(1)作DE⊥AB于E,连接BD,根据相似关系求出AE,而CD=AB-2AE,从而求出梯形ABCD的周长y与腰长x间的函数解析式,根据AD>0,AE>0,CD>0可求出定义域;
(2)利用二次函数在给定区间上求出最值的知识可求出函数的最大值.
解答:解:(1)如图,作DE⊥AB于E,连接BD.
因为AB为直径,所以∠ADB=90°.(1分)
在Rt△ADB与Rt△AED中,∠ADB=90°=∠AED,∠BAD=∠DAE,
所以Rt△ADB∽Rt△AED.(3分)
所以 ,即
,即 .
.
又AD=x,AB=4,所以 .(5分)
.(5分)
所以 ,(6分)
,(6分)
于是 (7分)
(7分)
由于AD>0,AE>0,CD>0,所以 ,
,
解得 .(9分)
.(9分)
故所求的函数为 .(10分)
.(10分)
(2)因为 ,(12分)
,(12分)
又 ,所以,当x=2时,y有最大值10.(14分)
,所以,当x=2时,y有最大值10.(14分)
点评:射影定理的应用是解决此题的关键,二次函数在解决实际问题中求解最值的常用的方法,属于中档题.
(2)利用二次函数在给定区间上求出最值的知识可求出函数的最大值.
解答:解:(1)如图,作DE⊥AB于E,连接BD.

因为AB为直径,所以∠ADB=90°.(1分)
在Rt△ADB与Rt△AED中,∠ADB=90°=∠AED,∠BAD=∠DAE,
所以Rt△ADB∽Rt△AED.(3分)
所以
 ,即
,即 .
.又AD=x,AB=4,所以
 .(5分)
.(5分)所以
 ,(6分)
,(6分)于是
 (7分)
(7分)由于AD>0,AE>0,CD>0,所以
 ,
,解得
 .(9分)
.(9分)故所求的函数为
 .(10分)
.(10分)(2)因为
 ,(12分)
,(12分)又
 ,所以,当x=2时,y有最大值10.(14分)
,所以,当x=2时,y有最大值10.(14分)点评:射影定理的应用是解决此题的关键,二次函数在解决实际问题中求解最值的常用的方法,属于中档题.

练习册系列答案
相关题目
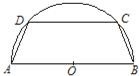 如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是圆O的直径,上底CD的端点在圆周上.
如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是圆O的直径,上底CD的端点在圆周上.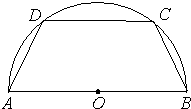 如图,有一块半径为2的半圆形钢板,现将其裁剪为等腰梯形ABCD的形状.它的下底AB是圆O的直径,上底CD的端点在圆周上.
如图,有一块半径为2的半圆形钢板,现将其裁剪为等腰梯形ABCD的形状.它的下底AB是圆O的直径,上底CD的端点在圆周上.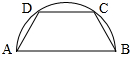 如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是圆的直径,上底CD的端点在圆周上,写出这个梯形周长y和腰长x间的函数解析式,定义域,并求出周长的最大值.
如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是圆的直径,上底CD的端点在圆周上,写出这个梯形周长y和腰长x间的函数解析式,定义域,并求出周长的最大值.