题目内容
 (附加题)试求函数y=sinx+cosx+2sinxcosx+2的最大值和最小值.
(附加题)试求函数y=sinx+cosx+2sinxcosx+2的最大值和最小值.
解:设sinx+cosx=t则 2sinxcosx=t2-1…(2分)
其中 …(4分)
…(4分)
所以函数化为 ,
, …(6分)
…(6分)
所以,当t=- 时,
时, .当
.当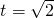 时,
时, …(10分)
…(10分)
分析:利用换元法,设sinx+cosx=t则 2sinxcosx=t2-1,从而将函数转化为t的函数,利用配方法,注意变量的范围,即可求得函数的最大值和最小值.
点评:本题以三角函数为载体,考查函数的最值,考查配方法的运用.换元是关键,别忘了变量范围的变化
其中
 …(4分)
…(4分)所以函数化为
 ,
, …(6分)
…(6分)所以,当t=-
 时,
时, .当
.当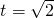 时,
时, …(10分)
…(10分)分析:利用换元法,设sinx+cosx=t则 2sinxcosx=t2-1,从而将函数转化为t的函数,利用配方法,注意变量的范围,即可求得函数的最大值和最小值.
点评:本题以三角函数为载体,考查函数的最值,考查配方法的运用.换元是关键,别忘了变量范围的变化

练习册系列答案
相关题目
 (附加题)试求函数y=sinx+cosx+2sinxcosx+2的最大值和最小值.
(附加题)试求函数y=sinx+cosx+2sinxcosx+2的最大值和最小值.