题目内容
(本小题满分12分)已知数列
(1)证明数列 为等差数列,并求
为等差数列,并求 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和。
项和。

(1)证明数列
 为等差数列,并求
为等差数列,并求 的通项公式;
的通项公式;(2)设
 ,求数列
,求数列 的前
的前 项和。
项和。(1)证明略, 的通项公式是
的通项公式是
(2)
 的通项公式是
的通项公式是
(2)

解:(I)因为
所以
两式相减,得

即
 …………3分
…………3分
又 ,
,
所以
 是首项为3,公比为3的等比数列,
是首项为3,公比为3的等比数列,
从而 的通项公式是
的通项公式是 …………6分
…………6分
(II)由(I)知 的前n项和为Tn。
的前n项和为Tn。
则

两式相减得
 …………10分
…………10分
 ,
,
所以 …………12分
…………12分

所以

两式相减,得


即

 …………3分
…………3分又
 ,
,所以

 是首项为3,公比为3的等比数列,
是首项为3,公比为3的等比数列,从而
 的通项公式是
的通项公式是 …………6分
…………6分(II)由(I)知
 的前n项和为Tn。
的前n项和为Tn。则


两式相减得
 …………10分
…………10分 ,
,所以
 …………12分
…………12分
练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 的前
的前 项和记为
项和记为
 ,已知
,已知 .
. ;
; ,求
,求 ,求证:数列
,求证:数列 为等比数列.
为等比数列. 满足,
满足,  .
. 令
令 ,证明:
,证明: 是等比数列; (Ⅱ)求
是等比数列; (Ⅱ)求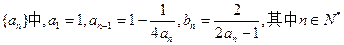 。
。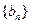 是等差数列,并求数列
是等差数列,并求数列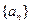 的通项公式;
的通项公式;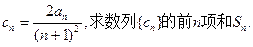
 的前
的前
 项和为
项和为 ,且
,且
 的值;
的值; 的数列前n项和为
的数列前n项和为 ,若
,若 ,则
,则 的值为( )
的值为( )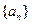 中,
中,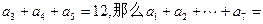 ( )
( ) 满足
满足 ,则它的前10项的和
,则它的前10项的和 ( )
( )