题目内容
已知一个圆截y轴所得的弦长为2,被x轴分成的两段弧长的比为3:1.(1)设圆心(a,b),求实数a、b满足的关系式;
(2)当圆心到直线l:x-2y=0的距离最小时,求圆的方程.
【答案】分析:(1)设出圆心P的坐标和半径为r,根据圆被x轴分成的两条弧之比得到 |b|=r,两边平方得到一个关系式,记作①式,再根据弦长的一半,弦心距即为P的横坐标的绝对值,及圆的半径r,利用勾股定理列出另外一个关系式,记作②,两式联立消去r即可得到a与b满足的关系式;
|b|=r,两边平方得到一个关系式,记作①式,再根据弦长的一半,弦心距即为P的横坐标的绝对值,及圆的半径r,利用勾股定理列出另外一个关系式,记作②,两式联立消去r即可得到a与b满足的关系式;
(2)先利用点到直线的距离公式表示出圆心P到直线l的距离d,两边平方后,根据基本不等式及(1)得出的a与b的关系式即可得到d的最小值,当且仅当a=b取等号,把a=b与(1)得出的关系式联立组成方程组,求出方程组的解得到a与b的值,进而确定出圆心坐标和圆的半径,写出圆的标准方程即可.
解答:解:(1)设圆心P(a,b),半径为r,则|b|= ,2b2=r2,①…(3分)
,2b2=r2,①…(3分)
又|a|2+1=r2,所以a2+1=r2,②
联立①②消去r得:2b2=a2+1;…(6分)
(2)点P到直线x-2y=0的距离d= ,
,
5d2=a2-4ab+4b2≥a2+4b2-2(a2+b2)=2b2-a2=1,…(9分)
所以 ,
,
所以 ,或
,或 ,…(11分)
,…(11分)
所以(x-1)2+(y-1)2=2或(x+1)2+(y+1)2=2.…(13分)
点评:此题考查了直线与圆的位置关系,涉及的知识有:垂径定理,勾股定理,点到直线的距离公式,基本不等式以及圆的标准方程,当直线与圆相交时,常常由弦长的一半,圆的半径及弦心距构造直角三角形,利用勾股定理来解决问题.
 |b|=r,两边平方得到一个关系式,记作①式,再根据弦长的一半,弦心距即为P的横坐标的绝对值,及圆的半径r,利用勾股定理列出另外一个关系式,记作②,两式联立消去r即可得到a与b满足的关系式;
|b|=r,两边平方得到一个关系式,记作①式,再根据弦长的一半,弦心距即为P的横坐标的绝对值,及圆的半径r,利用勾股定理列出另外一个关系式,记作②,两式联立消去r即可得到a与b满足的关系式;(2)先利用点到直线的距离公式表示出圆心P到直线l的距离d,两边平方后,根据基本不等式及(1)得出的a与b的关系式即可得到d的最小值,当且仅当a=b取等号,把a=b与(1)得出的关系式联立组成方程组,求出方程组的解得到a与b的值,进而确定出圆心坐标和圆的半径,写出圆的标准方程即可.
解答:解:(1)设圆心P(a,b),半径为r,则|b|=
 ,2b2=r2,①…(3分)
,2b2=r2,①…(3分)又|a|2+1=r2,所以a2+1=r2,②
联立①②消去r得:2b2=a2+1;…(6分)
(2)点P到直线x-2y=0的距离d=
 ,
,5d2=a2-4ab+4b2≥a2+4b2-2(a2+b2)=2b2-a2=1,…(9分)
所以
 ,
,所以
 ,或
,或 ,…(11分)
,…(11分)所以(x-1)2+(y-1)2=2或(x+1)2+(y+1)2=2.…(13分)
点评:此题考查了直线与圆的位置关系,涉及的知识有:垂径定理,勾股定理,点到直线的距离公式,基本不等式以及圆的标准方程,当直线与圆相交时,常常由弦长的一半,圆的半径及弦心距构造直角三角形,利用勾股定理来解决问题.

练习册系列答案
相关题目
 已知F1、F2为椭圆的焦点,P为椭圆上的任意一点,椭圆的离心率为
已知F1、F2为椭圆的焦点,P为椭圆上的任意一点,椭圆的离心率为 .以P为圆心PF2长为半径作圆P,当圆P与x轴相切时,截y轴所得弦长为
.以P为圆心PF2长为半径作圆P,当圆P与x轴相切时,截y轴所得弦长为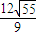 .
.