Question

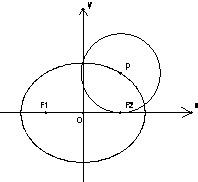已知F₁、F₂为椭圆的焦点，P为椭圆上的任意一点，椭圆的离心率为

1

3

．以P为圆心PF₂长为半径作圆P，当圆P与x轴相切时，截y轴所得弦长为

12 55

9

．
（1）求圆P方程和椭圆方程；
（2）求证：无论点P在椭圆上如何运动，一定存在一个定圆与圆P相切，试求出这个定圆方程．

Answer 1

分析：（1）根据离心率求得a和c的关系，进而求得b和c的关系，设出椭圆的标准方程，根据圆P与x轴相切时，PF₂⊥x轴，求得P的坐标和圆的半径，进而根据弦长公式求得c，则椭圆的方程可得．
（2）以F₁为圆心，作圆M，使得圆P内切于圆M，公切点设为Q，则可推断出点F₁、P、Q在一直线上，进而可知F₁Q=F₁P+PQ=F₁P+PF₂，求得a，进而可推断出存在圆M：（x+2）²+y²=36满足题设要求．

解答：解：（1）∵e=

1

3

，∴a=3c，b=2

2

c，
椭圆方程设为

x2

9c2

+

y2

8c2

=1，
当圆P与x轴相切时，PF₂⊥x轴，故求得P（c，±

8

3

c），圆半径r=

8

3

c，
由2

r2-c2

=

12 55

9

得c=2，
∴椭圆方程为

x2

36

+

y2

32

=1，
此时圆P方程为(x-2)2+(y±

16

3

)2=

256

9

．
（2）以F₁为圆心，作圆M，使得圆P内切于圆M，公切点设为Q，
则点F₁、P、Q在一直线上，
从而F₁Q=F₁P+PQ=F₁P+PF₂=2a=12，
∴存在圆M：（x+2）²+y²=144满足题设要求．

点评：本题主要考查了椭圆的应用，椭圆与圆的位置关系等．考查了分析问题和解决问题的能力．