题目内容
 如图,直三棱柱
如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 上的一点,
上的一点,![]() .
.
(Ⅰ)证明:![]() 为异面直线
为异面直线![]() 与
与![]() 的公垂线;
的公垂线;
(Ⅱ)设异面直线![]() 与
与![]() 的夹角为45°,求二面角
的夹角为45°,求二面角![]() 的大小.
的大小.
【命题意图】本试题主要考查空间的线面关系与空间角的求解,考查考生的空间想象与推理计算的能力.
【参考答案】
(19)解法一:
(I)连接A1B,记A1B与AB1的交点为F.
因为面AA1BB1为正方形,故A1B⊥AB1,且AF=FB1,又AE=3EB1,所以FE=EB1,又D为BB1的中点,故DE∥BF,DE⊥AB1. ………………3分
作CG⊥AB,G为垂足,由AC=BC知,G为AB中点.
又由底面ABC⊥面AA1B1B.连接DG,则DG∥AB1,故DE⊥DG,由三垂线定理,得DE⊥CD.
所以DE为异面直线AB1与CD的公垂线.
(II)因为DG∥AB1,故∠CDG为异面直线AB1与CD的夹角,∠CDG=45°
设AB=2,则AB1=![]() ,DG=
,DG=![]() ,CG=
,CG=![]() ,AC=
,AC=![]() .
.
作B1H⊥A1C1,H为垂足,因为底面A1B1C1⊥面AA1CC1,故B1H⊥面AA1C1C.又作HK⊥AC1,K为垂足,连接B1K,由三垂线定理,得B1K⊥AC1,因此∠B1KH为二面角A1-AC1-B1的平面角.



【点评】三垂线定理是立体几何的最重要定理之一,是高考的的热点,它是处理线线垂直问题的有效方法,同时它也是确定二面角的平面角的主要手段.通过引入空间向量,用向量代数形式来处理立体几何问题,淡化了传统几何中的“形”到“形”的推理方法,从而降低了思维难度,使解题变得程序化,这是用向量解立体几何问题的独到之处.

练习册系列答案
相关题目

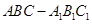 中,
中,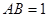 ,
,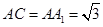 ,
,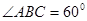 .
.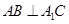 ;
;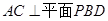
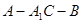 的正切值.
的正切值. 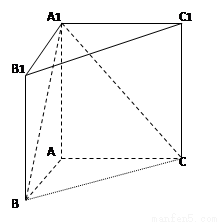
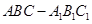 中,
中,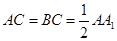 ,
,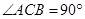 ,
,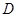 是棱
是棱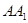 的中点.
的中点. ;
;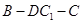 的余弦值。
的余弦值。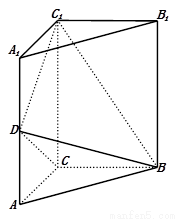
 中,
中,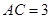 ,
,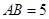 ,
,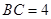
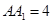 ,点
,点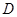 是
是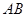 的中点.
的中点.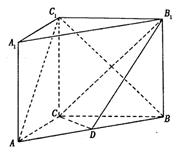
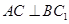 ;
;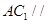 平面
平面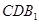 ;
;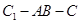 的正切值.
的正切值. 中,
中, ,
, ,点
,点 是
是 的中点,
的中点, ;
; ;
; 与平面
与平面 所成角的正切值.
所成角的正切值.