题目内容
19.过点A(0,8)且与圆C:x2+y2+10x+10y=0相切于原点的圆的标准方程为(x-4)2+(y-4)2 =32.分析 设所求的圆的圆心为M,可得M、O、C共线,故圆心M在直线y=x上,设所求的圆的圆心为M(a,a),又所求的圆过点A(0,8),可得圆心M还在直线y=4上,故M(4,4),求得半径AM的值,可得要求的圆的方程.
解答 解:圆C:x2+y2+10x+10y=0,即:(x+5)2+(y+5)2 =50,故圆心C(-5,-5).
根据两圆相切于原点,设所求的圆的圆心为M,可得M、O、C共线,
故圆心M在直线y=x上,设所求的圆的圆心为M(a,a),
又所求的圆过点A(0,8),故圆心M还在直线y=4上,故M(4,4),半径为AM=4$\sqrt{2}$,
故要求的圆的方程为:(x-4)2+(y-4)2 =32,
故答案为:(x-4)2+(y-4)2 =32.
点评 此题考查了直线与圆相交的性质,涉及的知识有圆的标准方程,垂径定理,勾股定理,两圆相切的性质,属于中档题.

练习册系列答案
相关题目
10.在集合{1,2,3,4}中任取一个偶数a和一个奇数b构成以原点为起点的向量$\overrightarrow{α}$=(a,b).从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形.记所有作成的平行四边形的个数为n,其中面积不超过4的平行四边形的个数为m,则$\frac{m}{n}$=( )
| A. | $\frac{4}{15}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{2}{3}$ |
9.已知sinα+cosα=$\frac{1}{2}$,α∈(0,π),则$\frac{1-tanα}{1+tanα}$=( )
| A. | $\sqrt{7}$ | B. | -$\sqrt{7}$ | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
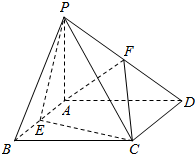 如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,E、F别是AB、PD的中点.若PA=AD=CD=4.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,E、F别是AB、PD的中点.若PA=AD=CD=4.