题目内容
14.在正方体ABCD-A1B1C1D1中,E为AB的中点,F为A1A的中点,则直线D1F与CE的位置关系是异面.(填平行、异面、相交三者之一)分析 取A1B1中点M,连结C1M,则CE∥C1M,由异面直线判定定理得D1F与C1M是异面直线,从而昨到直线D1F与CE的位置关系是异面.
解答  解:取A1B1中点M,连结C1M,
解:取A1B1中点M,连结C1M,
∵在正方体ABCD-A1B1C1D1中,E为AB的中点,F为A1A的中点,
∴CE∥C1M,
∵FD1∩平面A1C1=D1,D1∉C1M,
∴由异面直线判定定理得D1F与C1M是异面直线,
∴直线D1F与CE的位置关系是异面.
故答案为:异面.
点评 本题考查两条直线的位置关系的判断,是基础题,解题时要认真审题,注意异面直线判定定理的合理运用.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
5.已知复数z=$\frac{2+i}{i^3}$,z的共轭复数是$\overline{z}$,则$\overline{z}$对应的点位于复平面内的( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
2.函数$y=\frac{{{{(x-1)}^0}}}{{\sqrt{|x|+x}}}$的定义域是( )
| A. | (0,+∞) | B. | (0,1)∪(1,+∞) | C. | (-∞,0) | D. | (-∞,-1)∪(0,+∞) |
9.直线l的极坐标方程为ρcosθ-$\sqrt{3}$ρsinθ=5,圆C的参数方程为$\left\{\begin{array}{l}{x=5+2cosα}\\{y=4+2sinα}\end{array}\right.$(α为参数,α∈[0,2π)),则直线l与圆C的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 无法确定 |
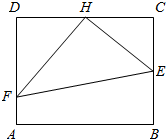 某高校专家楼前现有一块矩形草坪ABCD,已知草坪长AB=100米,宽BC=50$\sqrt{3}$米,为了便于专家平时工作、起居,该高校计划在这块草坪内铺设三条小路HE、HF和EF,并要求H是CD的中点,点E在边BC上,点F在边AD上,且∠EHF为直角,如图所示.
某高校专家楼前现有一块矩形草坪ABCD,已知草坪长AB=100米,宽BC=50$\sqrt{3}$米,为了便于专家平时工作、起居,该高校计划在这块草坪内铺设三条小路HE、HF和EF,并要求H是CD的中点,点E在边BC上,点F在边AD上,且∠EHF为直角,如图所示.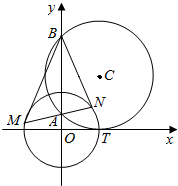 如图,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2.过点A任作一条直线与圆O:x2+y2=1相交于M,N两点,则$\frac{|NB|}{|NA|}$-$\frac{|MA|}{|MB|}$=2.
如图,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2.过点A任作一条直线与圆O:x2+y2=1相交于M,N两点,则$\frac{|NB|}{|NA|}$-$\frac{|MA|}{|MB|}$=2.