题目内容
平行四边形ABCD中,点E,F分别是AD,DC的中点,BE,BF分别与AC交于R,T两点,用向量的方法找出AR、RT、TC之间的关系.
 解:如图:
解:如图:由点E、R、B共线,可得
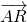 =λ
=λ +(1-λ)
+(1-λ) =
=
 +(1-λ)
+(1-λ) ,
,又由A、R、C共线,可得
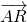 =μ
=μ =μ(
=μ( +
+ ),
),由平面向量基本定理知:μ=
 =1-λ,
=1-λ,∴λ=
 ,μ=
,μ= ,即AR=
,即AR= AC,
AC,同理可得CT=
 AC,
AC,∴AR=RT=TC.
分析:由点E、R、B共线,可得
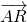 =
=
 +(1-λ)
+(1-λ) ,又由A、R、C共线,可得
,又由A、R、C共线,可得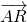 =μ
=μ =μ(
=μ( +
+ ),进而可得AR=
),进而可得AR= AC,同理可得CT=
AC,同理可得CT= AC,故可得答案.
AC,故可得答案.点评:本题考查平面向量基本定理和向量的基本运算,属中档题.

练习册系列答案
相关题目
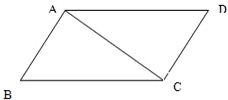 如图,在平行四边形ABCD中,AB=AC=1,∠ACD=90°,将它沿对角线AC折起,使AB与CD成60°角,则此时B、D的距离是 ( )
如图,在平行四边形ABCD中,AB=AC=1,∠ACD=90°,将它沿对角线AC折起,使AB与CD成60°角,则此时B、D的距离是 ( )A、2或
| ||
B、2或
| ||
| C、2 | ||
D、1或
|
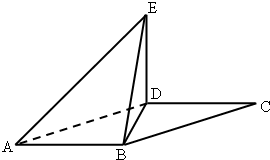 如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4将△CBD沿BD折起到△EBD的位置,使平面EDB⊥平面ABD.
如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4将△CBD沿BD折起到△EBD的位置,使平面EDB⊥平面ABD.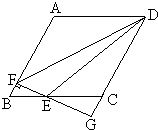 如图,在平行四边形ABCD中,AB=4,BC=3,∠BAD=120°,E为BC上一动点(不与B重合),作EF⊥AB于F,FE的延长线交DC的延长线于点G,设BE=x,△DEF的面积为S.
如图,在平行四边形ABCD中,AB=4,BC=3,∠BAD=120°,E为BC上一动点(不与B重合),作EF⊥AB于F,FE的延长线交DC的延长线于点G,设BE=x,△DEF的面积为S.