题目内容
 如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别为棱A1B1和B1C1的中点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别为棱A1B1和B1C1的中点.(1)求二面角B1-BF-E的大小.
(2)求点D到平面BEF的距离.
(3)能否在棱B1B上找到一点M,使DM⊥面BEF?若能,请确定点M的位置;若不能,请说明理由.
分析:(1)过B1作B1G⊥BF于G,连接EG,则由EB1⊥面B1BCC1,可知EG⊥BF.即∠B1GE是二面角B1-BF-E的平面角.解三角形B1GE即可得到二面角B1-BF-E的大小;
(2)连接B1D1与EF交于N,可得面BEF⊥面BB1D1D,且面BEF∩面BB1D1D=BN.过D作DH⊥BN于H,则DH⊥面BEF.即DH的长即为点D到面BEF的距离.根据△BDH∽△NBB1,结合相似三角形的性质,我们根据相似三角形对应边成比例,即可求出点D到平面BEF的距离.
(3)在平面BB1D1D中,延长DH交BB1于M,由(2),DH⊥面BEF,则DM⊥面BEF.然后根据△BDM∽△B1BN,结合相似三角形对应边长成比例,易得到结论.
(2)连接B1D1与EF交于N,可得面BEF⊥面BB1D1D,且面BEF∩面BB1D1D=BN.过D作DH⊥BN于H,则DH⊥面BEF.即DH的长即为点D到面BEF的距离.根据△BDH∽△NBB1,结合相似三角形的性质,我们根据相似三角形对应边成比例,即可求出点D到平面BEF的距离.
(3)在平面BB1D1D中,延长DH交BB1于M,由(2),DH⊥面BEF,则DM⊥面BEF.然后根据△BDM∽△B1BN,结合相似三角形对应边长成比例,易得到结论.
解答: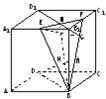 解:(1)过B1作B1G⊥BF于G,连接EG,
解:(1)过B1作B1G⊥BF于G,连接EG,
则由EB1⊥面B1BCC1,可知EG⊥BF.
∴∠B1GE是二面角B1-BF-E的平面角.
在Rt△BB1F中,B1B=a,B1F=
,
∴BF=
=
a,
B1G=
=
=
a.
在Rt△B1GE中,B1E=
,B1G=
a,
∴tan∠B1GE=
=
=
.
∴∠B1GE=arctan
.
故二面角B1-BF-E的大小为arctan
.
(2)连接B1D1与EF交于N,
则EF⊥B1D1.又BB1⊥EF,
∴EF⊥面BB1D1D.又EF?面BEF,
∴面BEF⊥面BB1D1D,且面BEF∩面BB1D1D=BN.
过D作DH⊥BN于H,则DH⊥面BEF.
∴DH的长即为点D到面BEF的距离.
在矩形BB1D1D中,
易证△BDH∽△NBB1,
∴
=
,DH=
=
=
a.
故点D到面BEF的距离为
a.
(3)在平面BB1D1D中,延长DH交BB1于M,由(2),DH⊥面BEF,
∴DM⊥面BEF.
由△BDM∽△B1BN,有
=
,
∴BM=
=
=
.
则M为BB1的中点.
故在棱BB1上可找到点M,使DM⊥面BEF,此时M为BB1的中点.
 解:(1)过B1作B1G⊥BF于G,连接EG,
解:(1)过B1作B1G⊥BF于G,连接EG,则由EB1⊥面B1BCC1,可知EG⊥BF.
∴∠B1GE是二面角B1-BF-E的平面角.
在Rt△BB1F中,B1B=a,B1F=
| a |
| 2 |
∴BF=
| B1B2+B1F2 |
| ||
| 2 |
B1G=
| B1B•B1F |
| BF |
a×
| ||||
|
| ||
| 5 |
在Rt△B1GE中,B1E=
| a |
| 2 |
| ||
| 5 |
∴tan∠B1GE=
| B1E |
| B1G |
| ||||
|
| ||
| 2 |
∴∠B1GE=arctan
| ||
| 2 |
故二面角B1-BF-E的大小为arctan
| ||
| 2 |
(2)连接B1D1与EF交于N,
则EF⊥B1D1.又BB1⊥EF,
∴EF⊥面BB1D1D.又EF?面BEF,
∴面BEF⊥面BB1D1D,且面BEF∩面BB1D1D=BN.
过D作DH⊥BN于H,则DH⊥面BEF.
∴DH的长即为点D到面BEF的距离.
在矩形BB1D1D中,
易证△BDH∽△NBB1,
∴
| DH |
| BB1 |
| DB |
| BN |
| BB1•DB |
| BN |
a×
| ||||
|
| 4 |
| 3 |
故点D到面BEF的距离为
| 4 |
| 3 |
(3)在平面BB1D1D中,延长DH交BB1于M,由(2),DH⊥面BEF,
∴DM⊥面BEF.
由△BDM∽△B1BN,有
| BM |
| B1N |
| BD |
| BB1 |
∴BM=
| BD•B1N |
| BB1 |
| ||||||
| a |
| a |
| 2 |
则M为BB1的中点.
故在棱BB1上可找到点M,使DM⊥面BEF,此时M为BB1的中点.
点评:求二面角的大小,一般先作出二面角的平面角.此题是利用二面角的平面角的定义作出∠B1GE是二面角B1-BF-E的平面角,通过解∠B1GE所在的三角形求得∠B1GE.其解题过程为:作∠B1GE→证∠B1GE是二面角的平面角→计算∠B1GE,简记为“作、证、算”.

练习册系列答案
相关题目
 如图,在棱长为2的正四面体A-BCD中,若以△ABC为视角正面,则其正视图的面积是( )
如图,在棱长为2的正四面体A-BCD中,若以△ABC为视角正面,则其正视图的面积是( ) ,当
,当 取什么位置时,三棱柱的体积最大?
取什么位置时,三棱柱的体积最大?





