题目内容
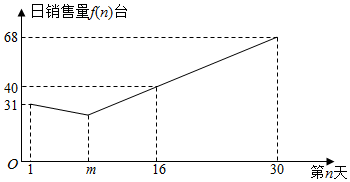
10.某电器专卖店销售某种型号的空调,记第n天(1≤n≤30,n∈N+)的日销售量为f(n)(单位;台).函数f(n)图象中的点分别在两条直线上,如图,该两直线交点的横坐标为m(m∈N+),已知1≤n≤m时,函数f(n)=32-n.(1)当m≤n≤30时,求函数f(n)的解析式;
(2)求m的值及该店前m天此型号空调的销售总量;
(3)按照经验判断,当该店此型号空调的销售总量达到或超过570台,且日销售量仍持续增加时,该型号空调开始旺销,问该店此型号空调销售到第几天时,才可被认为开始旺销?
分析 (1)根据题意,当m≤n≤30时,设f(n)=kn+b,(n∈N*),利用f(16)=40,f(30)=68,求出参数,进而得到f (n)的表达式;
(2)利用1≤n≤m时,函数f(n)=32-n;当m≤n≤30时,f(n)=2n+8,建立方程,求出m,利用等差数列的求和公式求出前m天此型号空调的销售总量;
(3)设该店此型号空调销售到第x天时,才可被认为开始旺销,则销售总量220+$\frac{(x-8)(26+2x+8)}{2}$≥570,求出x,即可得出结论.
解答 解:(1)根据题意,当m≤n≤30时,设f(n)=kn+b,(n∈N*)
∵f(16)=40,f(30)=68,
∴$\left\{\begin{array}{l}{16k+b=40}\\{30k+b=68}\end{array}\right.$,∴k=2,b=8,
∴f(n)=2n+8(m≤n≤30),
(2)∵1≤n≤m时,函数f(n)=32-n;当m≤n≤30时,f(n)=2n+8,
∴32-m=2m+8,∴m=8.
∴该店前m天此型号空调的销售总量$\frac{8(31+24)}{2}$=220台;
(3)设该店此型号空调销售到第x天时,才可被认为开始旺销,则销售总量220+$\frac{(x-8)(26+2x+8)}{2}$≥570,
∴x2+9x-386≥0,∴x≥18,
∴设该店此型号空调销售到第18天时,才可被认为开始旺销.
点评 已知函数图象求函数的解析式,是一种常见的题型,关键是要知道函数的类型,利用待定系数法设出函数的解析式,然后将函数图象上的点的坐标代入求出参数的值,即可得到要求函数的解析式.

练习册系列答案
相关题目
20.植树节期间我市组织义工参加植树活动,为方便安排任务将所有义工按年龄分组:第l组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的部分频率分布表如下:
(1)求a,b的值;
(2)现在要从年龄较小的第l,2,3组中用分层抽样的方法随机抽取6人担任联系人,在第l,2,3组抽取的义工的人数分别是多少?
(3)在(2)的条件下,从这6人中随机抽取2人担任本次活动的宣传员,求至少有1人年龄在第3组的概率.
| 区间 | 人数 | 频率 | |
| 第1组 | [25,30) | 50 | 0.1 |
| 第2组 | [30,35) | 50 | 0.1 |
| 第3组 | [35,40) | a | 0.4 |
| 第4组 | [40,45) | 150 | b |
(2)现在要从年龄较小的第l,2,3组中用分层抽样的方法随机抽取6人担任联系人,在第l,2,3组抽取的义工的人数分别是多少?
(3)在(2)的条件下,从这6人中随机抽取2人担任本次活动的宣传员,求至少有1人年龄在第3组的概率.
19.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的实轴为A1A2,虚轴的一个端点为B,若三角形A1A2B的面积为$\sqrt{2}$b2,则双曲线的离心率( )
| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
