题目内容
已知偶函数 满足:当
满足:当 时,
时, ,当
,当 时,
时, .
.
(Ⅰ).求 表达式;
表达式;
(Ⅱ).若直线 与函数
与函数 的图像恰有两个公共点,求实数
的图像恰有两个公共点,求实数 的取值范围;
的取值范围;
(Ⅲ).试讨论当实数 满足什么条件时,直线
满足什么条件时,直线 的图像恰有
的图像恰有 个公共点
个公共点 ,且这
,且这 个公共点均匀分布在直线
个公共点均匀分布在直线 上.(不要求过程)
上.(不要求过程)
(Ⅰ).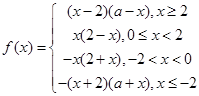 ;(Ⅱ).
;(Ⅱ).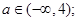 (Ⅲ).当
(Ⅲ).当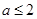 时,
时,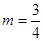 或
或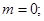
当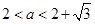 时,
时,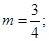 此时
此时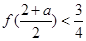 ; 当
; 当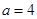 时,
时,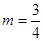 ,
, 或
或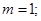
当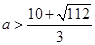 时
时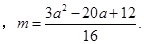 此时
此时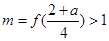 .
.
解析试题分析:(1)由 为偶函数,则有
为偶函数,则有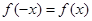 ,又因为当
,又因为当 ,
,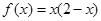 及
及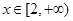 ,
, ,所以当
,所以当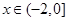 时,
时,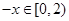 ,
,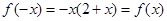 即可求出
即可求出 .当
.当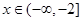 时,
时,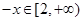 同理可求出此时的
同理可求出此时的 .(2)画出
.(2)画出 的大致图像,由图1易知,当
的大致图像,由图1易知,当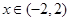 时,函数
时,函数 与
与 恰有两个交点,所以当
恰有两个交点,所以当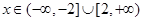 时,函数
时,函数 与
与 无交点,易得当
无交点,易得当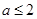 时恒成立,当
时恒成立,当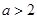 时,则有
时,则有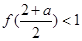 ,即可求出
,即可求出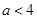 .
.
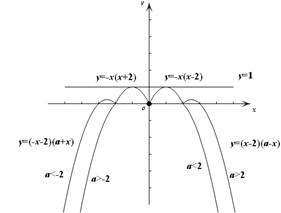
当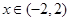 ,
,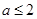 时,函数
时,函数 的图像如图2所示,此时直线
的图像如图2所示,此时直线 的图像若恰有
的图像若恰有 个公共点
个公共点 ,且这
,且这 个公共点均匀分布在直线
个公共点均匀分布在直线 上,则易知
上,则易知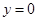 时符合题意,设
时符合题意,设 时由左到右的两个交点的横坐标分别为
时由左到右的两个交点的横坐标分别为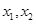 ,由函数的对称性易知,
,由函数的对称性易知,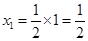 ,此时
,此时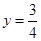 .其他情况同理即可求出.
.其他情况同理即可求出.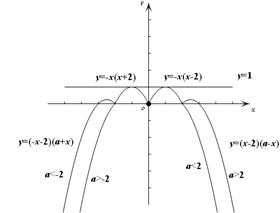
图1 图2
试题解析:(1)
 为偶函数,则有
为偶函数,则有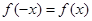
当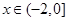 时,
时,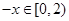 ,
,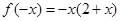 即
即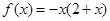
当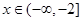 时,
时,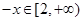 ,
,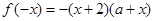 即
即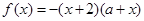
故有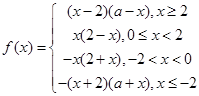
(2)如下图,当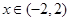 时,由图像易知函数
时,由图像易知函数 与
与 恰有两个交点
恰有两个交点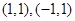
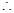 当
当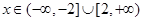 时,函数
时,函数 与
与 无交点
无交点
由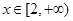 ,
,
当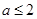 时,此时符合题意
时,此时符合题意
当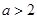 时,由
时,由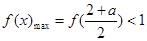 即
即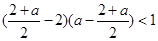
可得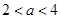
由偶函数的对称性可知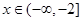 时,
时,
与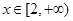 时的情况相同
时的情况相同
故综上: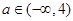
(3)当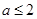

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 ,函数
,函数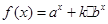
 且
且 ,
, 且
且 .
.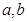 满足
满足 且
且 ,函数
,函数 是否具有奇偶性? 如果有,求出相应的
是否具有奇偶性? 如果有,求出相应的 值;如果没有,说明原因;
值;如果没有,说明原因; ,讨论函数
,讨论函数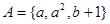 ,
,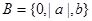 且
且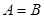 .
.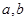 的值;
的值;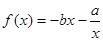 在
在 的单调性,并用定义加以证明.
的单调性,并用定义加以证明. ,当
,当 时,对应
时,对应 值的集合为
值的集合为 .
. 的值;(2)若
的值;(2)若 ,求该函数的最值.
,求该函数的最值.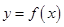 和
和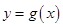 的图象关于
的图象关于 轴对称,且
轴对称,且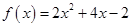 .
.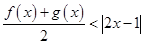 .
. 来拟合该景点对外开放的第
来拟合该景点对外开放的第
 年与当年的游客人数
年与当年的游客人数 (单位:万人)之间的关系.
(单位:万人)之间的关系. =
= ,试确定
,试确定 的值,并考察该函数是否符合上述两点预测;
的值,并考察该函数是否符合上述两点预测; ,欲使得该函数符合上述两点预测,试确定
,欲使得该函数符合上述两点预测,试确定 的取值范围.
的取值范围. 在[0,+∞)上是减函数,试比较
在[0,+∞)上是减函数,试比较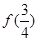 与
与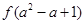 的大小.
的大小.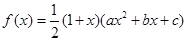 ,
,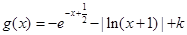
 的图像关于
的图像关于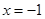 对称,且
对称,且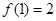 ,求
,求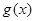 的图像的交点个数.
的图像的交点个数. (
( )在区间
)在区间 上有最大值
上有最大值 和最小值
和最小值 .设
.设 .
. 、
、 的值;
的值; 在
在 上有解,求实数
上有解,求实数 的取值范围.
的取值范围.