题目内容
已知数列{an}及其前n项和Sn满足:a1=3,Sn=2Sn-1+2n(n≥2,n∈N*).
(1)证明:设bn=
,{bn}是等差数列;
(2)求Sn及an.
(1)证明:设bn=
| Sn | 2n |
(2)求Sn及an.
分析:(1)由已知可得,
-
=1,即可证明
(2)由(1)可求sn,然后利用n≥2时,an=sn-sn-1可求an
| Sn |
| 2n |
| Sn-1 |
| 2n-1 |
(2)由(1)可求sn,然后利用n≥2时,an=sn-sn-1可求an
解答:(本题满分14分)
解:(1)∵Sn-2Sn-1=2n
∴
-
=1(n≥2)…(4分)
设bn=
则{bn}是公差为1的等差数列 …(6分)
(2)又∵b1=
=
=
,
∴
=n+
,
∴Sn=(n+
)2n…(9分)
当n≥2时,an=sn-sn-1=(2n+3)2n-2…(12分)
∴an=
Sn=(n+
)2n…(14分)
解:(1)∵Sn-2Sn-1=2n
∴
| Sn |
| 2n |
| Sn-1 |
| 2n-1 |
设bn=
| Sn |
| 2n |
(2)又∵b1=
| S1 |
| 2 |
| a1 |
| 2 |
| 3 |
| 2 |
∴
| Sn |
| 2n |
| 1 |
| 2 |
∴Sn=(n+
| 1 |
| 2 |
当n≥2时,an=sn-sn-1=(2n+3)2n-2…(12分)
∴an=
|
|
Sn=(n+
| 1 |
| 2 |
点评:本题主要考查了利用数列的递推公式构造等差数列求通项公式及数列的递推公式an=sn-sn-1的应用

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
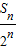 ,{bn}是等差数列;
,{bn}是等差数列;